主要内容 #
- 铺地毯
- 津津的储蓄计划
1. 铺地毯 #
1.1 问题描述
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有 n 张地毯,编号从 1 到 n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
1.2 输入格式
输入共 n+2 行。第一行,一个整数 n,表示总共有 n 张地毯。接下来的 n 行中,第 i+1 行表示编号 i 的地毯的信息,包含四个正整数 a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a,b)以及地毯在 x轴和 y 轴方向的长度。第 n+2 行包含两个正整数 x 和 y,表示所求的地面的点的坐标(x,y)。
1.3 输出格式
输出共1行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1
1.4 输入输出样例
输入
3
1 0 2 3
0 2 3 3
2 1 3 3
2 2
输出
3
1.5 分析
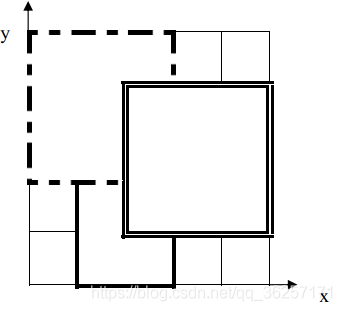
如上图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,覆盖点(2,2)的最上面一张地毯是 3 号地毯。那么我们可以使用 for循环 和 if判断语句 来解答此题。
1.6 参考代码
#include<iostream> //比赛可用C++万能头文件,也可用iostream库
using namespace std;
int a[10002],b[10002],g[10002],k[10002]; //定义数组;
int main()
{
int n,x,y,i,s=-1; //注意:由题可得,这里的累加器最初应定义-1
cin>>n;
for(i=1;i<=n;i++)
{
cin>>a[i]>>b[i]>>g[i]>>k[i]; //通过for循环输入
}
cin>>x>>y;
for(i=1;i<=n;i++)
{
if(x>=a[i]&&x<=a[i]+g[i]&&
y>=b[i]&&y<=b[i]+k[i]) //判断语句
s=i;
}
cout<<s;
return 0; //结束整个程序
}
2. 津津的储蓄计划 #
2.1 问题描述
津津的零花钱一直都是自己管理。每个月的月初妈妈给津津300元钱,津津会预算这个月的花销,并且总能做到实际花销和预算的相同。
为了让津津学习如何储蓄,妈妈提出,津津可以随时把整百的钱存在她那里,到了年末她会加上20%还给津津。因此津津制定了一个储蓄计划:每个月的月初,在得到妈妈给的零花钱后,如果她预计到这个月的月末手中还会有多于100元或恰好100元,她就会把整百的钱存在妈妈那里,剩余的钱留在自己手中。
例如11月初津津手中还有83元,妈妈给了津津300元。津津预计11月的花销是180元,那么她就会在妈妈那里存200元,自己留下183元。到了11月月末,津津手中会剩下3元钱。
津津发现这个储蓄计划的主要风险是,存在妈妈那里的钱在年末之前不能取出。有可能在某个月的月初,津津手中的钱加上这个月妈妈给的钱,不够这个月的原定预算。如果出现这种情况,津津将不得不在这个月省吃俭用,压缩预算。
现在请你根据2004年1月到12月每个月津津的预算,判断会不会出现这种情况。如果不会,计算到2004年年末,妈妈将津津平常存的钱加上20%还给津津之后,津津手中会有多少钱。
2.2 输入格式
12行数据,每行包含一个小于350的非负整数,分别表示1月到12月津津的预算。
2.3 输出格式
一个整数。如果储蓄计划实施过程中出现某个月钱不够用的情况,输出−X,X表示出现这种情况的第一个月;否则输出到2004年年末津津手中会有多少钱。
2.4 输入输出样例
输入
290
230
280
200
300
170
340
50
90
80
200
60
输出
-7
2.5 参考程序
#include<iostream>
using namespace std;
int a = 0, sum = 0; //表示目前津津手上的钱,sum 表示存在妈妈那里的錢
int main(){
int month; //month 表示每月的开支
for(int i = 1; i <= 12; ++i){
cin >> month;
a += 300; //每月得到的零花钱
if(a < month){ //判断手上的钱对于开支是否足够
cout << -i << endl; //如果不足则输出“-”加月份
return 0; //如果不足,输出后结束程序
}
a -= month; //如果够减去开支
if(a >= 100){
sum += 100*(a/100);//再把剩下的钱足整百的部分存入(加上a减去其除100的余数 即整百数)
a %= 100; //计算剩下的钱(因整百部分被存入,故a=其除以100后的余数)
}
}
cout << sum*1.2 + a << endl; //说明没有钱不足的情况,故应输出120%的储蓄加上手头的钱
return 0;
}



