汉诺塔问题 #

1. 汉诺塔问题的介绍及函数定义
2. 汉诺塔问题的递归的拆解
3. 递归的出口

汉诺塔问题的介绍及函数的定义 #

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

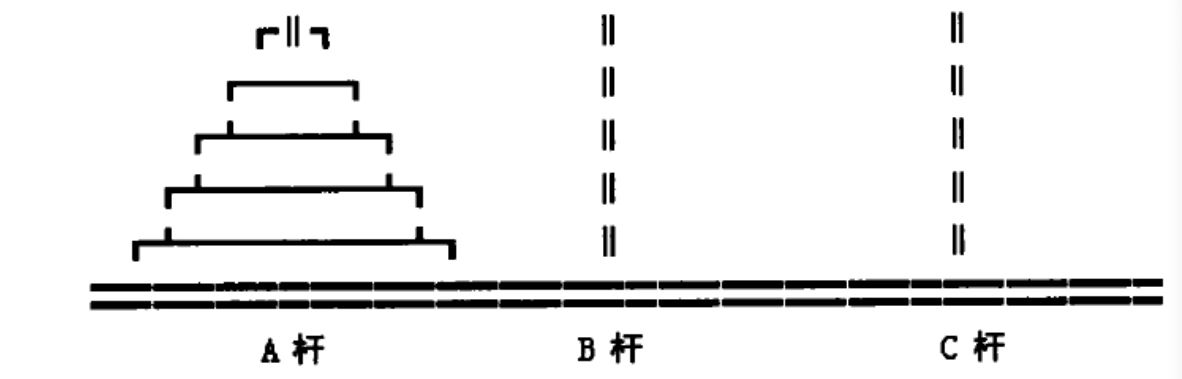
汉诺塔问题是一个非常典型的递归问题，如何求解金盘的移动轨迹呢？首先定义递归函数f(a,b,c,n),函数的功能:是以参数b杆为媒介将n个盘子从参数a杆移向参数c杆

def f(a,b,c,n):#功能:以参数b杆为媒介将n个盘子从参数a杆移向参数c杆
	pass

汉诺塔问题的递归的拆解 #

汉诺塔问题的拆解可以分为以下三步进行:

def f(a,b,c,n):
	f(a,c,b,n-1) #以参数c杆为中介，从a杆将1至n-1号盘移至b杆
	print(a+"->"+c)#将参数a杆中剩下的第n个盘子移向c杆
	f(b,a,c,n-1) #以参数a杆为中介；从b杆将1至n-1号盘移至c杆

递归的出口 #

每次递归我们都将n个金盘移动的问题，转化为n-1个金盘移动的问题，很容易能够想到当n=1时，只需将参数a杆的金盘移动到参数c杆即可

def f(a,b,c,n):#以参数b杆为媒介将n个盘子移向参数c杆
    if n==1:   #递归函数的出口,仅剩一个金盘只需将参数a杆的金盘移动到参数c杆
        print(a+"->"+c)
        return
    f(a,c,b,n-1) #以参数c杆为中介，从a杆将1至n-1号盘移至b杆
    print(a+"->"+c)#将参数a杆中剩下的第n个盘子移向c杆
    f(b,a,c,n-1) #以参数a杆为中介；从b杆将1至n-1号盘移至c杆

小结 #

习题 #

1. 画出上例中f(‘a’,’b’,’c’,3)递归调用执行过程图
2. 将上述递归函数的return改为下面的写法，可以吗？猜想并验证

def f(a,b,c,n):#以参数b杆为媒介将n个盘子移向参数c杆
    if n==1:
        print(a+"->"+c)
    else:
        f(a,c,b,n-1) #以参数c杆为中介，从a杆将1至n-1号盘移至b杆
        print(a+"->"+c)#将参数a杆中剩下的第n个盘子移向c杆
        f(b,a,c,n-1) #以参数a杆为中介；从b杆将1至n-1号盘移至c杆