主要内容 #

1. 连通块
2. 算法分析
3. 参考代码

1. 连通块 #

问题描述
一个n × m的方格图，一些格子被涂成了黑色，在方格图中被标为1，白色格子标为0。问有多少个四连通的黑色格子连通块。四连通的黑色格子连通块指的是一片由黑色格子组成的区域，其中的每个黑色格子能通过四连通的走法（上下左右），只走黑色格子，到达该联通块中的其它黑色格子。
输入描述
第一行两个整数n,m(1≤n,m≤100)，表示一个n × m的方格图。
接下来n行，每行m个整数，分别为0或1，表示这个格子是黑色还是白色。
输出描述
一行一个整数ans，表示图中有ans个黑色格子连通块。
输入样例
3 3
1 1 1
0 1 0
1 0 1
输出样例
3

2. 算法分析 #

我们可以枚举每个格子，且它不属于被搜索过的连通块，则由它开始，扩展搜索它所在的连通块，并把连通块里所有的黑色的格子标记为已搜索过。
如何扩展搜索一个连通块呢？我们用一个搜索队列，存储搜索的格子。每次取出队首的格子，对其进行四连通扩展，若有黑格子，将其加入队尾，扩展完就把该格子删除。当队列为空时，一个连通块就搜索完了。
如样例对应的方格图如下所示：

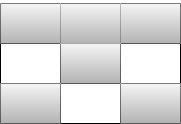
现在我们可以以样例为例模拟出这个方格图的搜索顺序：

• 将(1,1)加入队列，(1,1)表示左上角这个格子，当前队列为：{(1,1)}，连通块加1等于1。
• 取出队首的(1,1)，标记为已搜索并对其进行四连通扩展，扩展出(1,2)，删除(1,1)队列变为：{(1,2)}。
• 取出队首的(1,2)，标记为已搜索并对其进行四连通扩展，扩展到了(1,1)，(1,3)，(2,2)，(1,1)已经被搜索过，所以只将(1,3)，(2,2)加入队列，删除队首的(1,2)，队列变为：{(1,3),(2,2)}。
• 取出队首的(1,3)，没有扩展出新格子，删除队首，队列变为：{(2,2)}。
• 取出队首的(2,2)，将没有扩展出新格子，队列变为{}。完成以(1,1)开始的搜索。
• 将(3,1)加入队列，队列变为：{(3,1)}，连通块数加1变为2。
• 取出队首的(3,1),没有扩展出新的格子，删除队首，队列变为{}。完成以(3,1)开始的搜索。
• 将(3,3)加入队列，队列变为：{(3,3)}，连通块数加1变为3。
• 取出队首的(3,3),没有扩展出新的格子，删除队首，队列变为{}。完成以(3,3)开始的搜索。无法加入新的元素，程序结束。

3. 参考代码 #

#include<iostream>
using namespace std;

const int N = 110;
const int flag[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
int a[N][N], queue[N*N][2];
int n, m ,ans;
bool p[N][N];

void bfs(int x, int y){
    int front = 0, rear = 2;
    queue[1][0] = x, queue[1][1] = y;
    while(front < rear - 1){
        ++front;
        x = queue[front][0];
        y = queue[front][1];
        for(int i = 0; i < 4; ++i){
            int x1 = x + flag[i][0];
            int y1 = y + flag[i][1];
            if(x1<1||y1<1||x1>n||y1>m||!a[x1][y1]||p[x1][y1]) continue;
            p[x1][y1] = true;
            queue[rear][0] = x1;
            queue[rear++][1] = y1;
        }
    }
}

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
            cin >> a[i][j];
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
            if(a[i][j] && !p[i][j]){
                ++ans;
                bfs(i,j);
            }
    cout << ans << endl;
    return 0;
}