二叉排序树 #

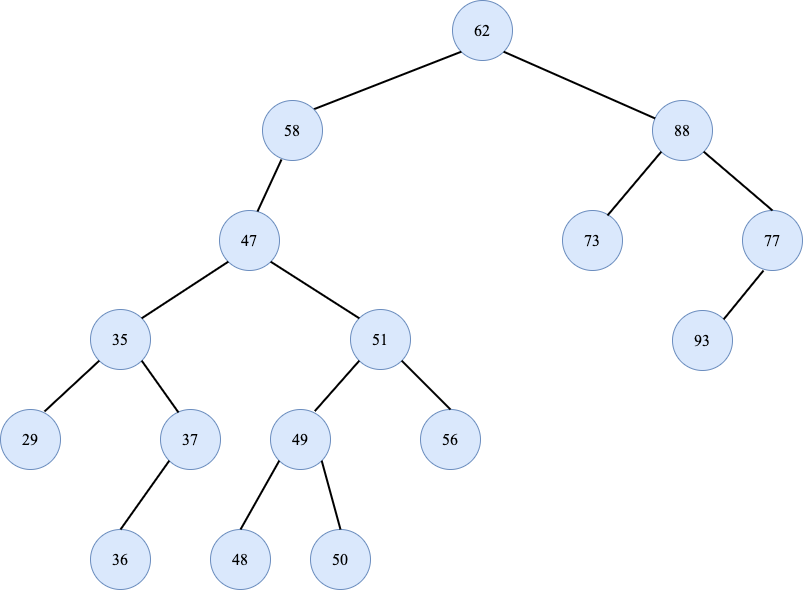
对于无序的序列“62，58，88，47，73，99，35，51，93，29，37，49，56，36，48，50”，是否存在一种高效的查找方案，使得能够快速判断在序列中是否存在指定的数值？二叉排序树是一种简单，高效的数据结构。
二叉排序树，又称为二叉查找树。二叉排序树或者是一棵空树，或者是具有以下性质的二叉树：若其左子树不为空，则左子树上的所有节点的值均小于它的根结点的值；若其右子树不为空，则右子树上的所有节点的值均大于它的根结点的值；左右子树又分别是二叉排序树。
对于以上的序列，我们构建如下的二叉排序树，其左子树小于根结点的值，右子树大于根结点的值：

二叉排序树的结构为：

typedef struct tree_node{
        double value;
        struct tree_node *left;
        struct tree_node *right;
}*node, binode;

二叉排序树的查找 #

二叉排序树的查找是指在二叉排序树中查找到对应的值，如在上述的二叉排序树中查找“49”，其具体过程为：

• 与根结点的值相比：49<52，查找其左子树 4
• 9<58，查找其左子树
• 49>47，查找其右子树
• 49<51，查找其左子树
• 49=49，查找成功

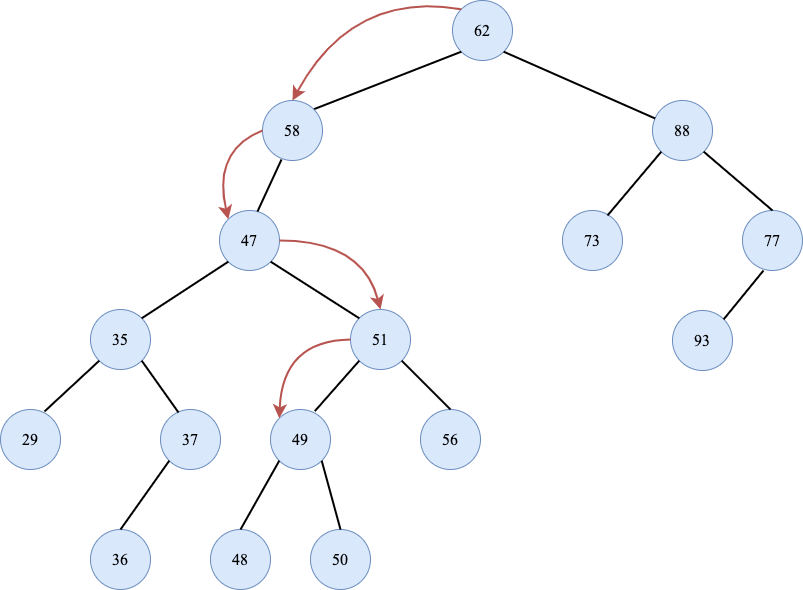
其具体过程如下图所示：

其具体实现过程为：

int search_value(node root, double a, node *p){
        if (NULL == root) {
                return 1; // 查找不成功
        }
        else if (a == root->value) {
                return 0; // 树中已经存在该节点
        }else if (a < root->value) {
                *p = root; // 记录父节点
                return search_value(root->left, a, p); //查找左子树
        }else {
                *p = root;
                return search_value(root->right, a, p); // 查找右子树
        }
}

二叉排序树的插入 #

对于插入操作，主要分为两种情况：

• 若二叉排序树中存在该值，则不做任何操作
• 若二叉排序树中不存在该值，则插入

插入的具体操作是判断与二叉排序树中节点的值，若小于当前节点的值，则选择左子树插入，若大于当前节点的值，则选择右子树插入；对于左右子树，进行同样的操作。
其实现过程为：

int insert_tree(node *root, double a){
        node p = *root;
        node q = NULL;
        printf("insert: %lf\n", a);

        if (search_value(*root, a, &p) == 1) { // 查找树中是否存在a
                q = (binode *)malloc(sizeof(binode)); // 不存在a，申请空间
                q->value = a;
                q->left = q->right = NULL;

                if (*root == NULL){ // 树为空
                        *root = q;
                }else {
                        if (a < p->value){
                                p->left = q; // 插入左子树
                        }else{
                                p->right = q; // 插入右子树
                        }
                }
                return 0;
        }
        return 1;
}