CSP-J 045 二叉树的遍历

4 min read

前序遍历 #

所谓前序或者先序遍历二叉树，指的是从根结点出发，按照以下步骤访问二叉树的每个结点：

访问当前结点；
进入当前结点的左子树，以同样的步骤遍历左子树中的结点；
遍历完当前结点的左子树后，再进入它的右子树，以同样的步骤遍历右子树中的结点；

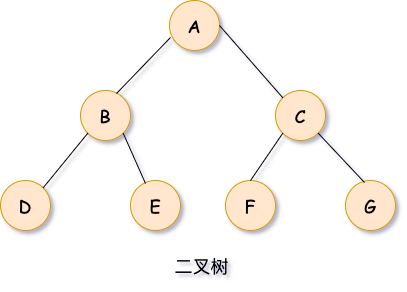
举个简单的例子，下图是一棵二叉树：

先序遍历这棵二叉树的过程是：

访问根节点 A；
进入 A 的左子树，执行同样的步骤：
    访问结点 B；
    进入 B 的左子树，执行同样的步骤：
        访问结点 D；
        结点 D 没有左子树；
        结点 D 没有右子树；
    进入 B 的右子树，执行同样的步骤：
        访问结点 E；
        结点 E 没有左子树；
        结点 E 没有右子树；
进入 A 的右子树，执行同样的步骤：
    访问结点 C；
    进入 C 的左子树，执行同样的步骤：
        访问结点 F；
        结点 F 没有左子树；
        结点 F 没有右子树；
    进入 C 的右子树，执行同样的步骤：
        访问结点 G；
        结点 G 没有左子树；
        结点 G 没有右子树

经过以上过程，就访问了二叉树中的各个结点，访问的次序是：
A B D E C F G

实现代码 #

观察整个先序遍历二叉树的过程会发现，访问每个结点的过程都是相同的，可以用递归的方式实现二叉树的先序遍历。
对于顺序表存储的二叉树，递归实现先序遍历二叉树的 C 语言代码为

#include <stdio.h>
#define NODENUM 7
#define ElemType int
//自定义 BiTree 类型，表示二叉树
typedef ElemType BiTree[NODENUM];

//存储二叉树
void InitBiTree(BiTree T) {
    ElemType node;
    int i = 0;
    printf("按照层次从左往右输入树中结点的值，0 表示空结点，# 表示输入结束:");
    while (scanf("%d", &node))
    {
        T[i] = node;
        i++;
    }
}

void PreOrderTraverse(BiTree T, int p_node) {
    //根节点的值不为 0，证明二叉树存在
    if (T[p_node]) {
        printf("%d ", T[p_node]);
        //先序遍历左子树
        if ((2 * p_node + 1 < NODENUM) && (T[2 * p_node + 1] != 0)) {
            PreOrderTraverse(T, 2 * p_node + 1);
        }
        //最后先序遍历右子树
        if ((2 * p_node + 2 < NODENUM) && (T[2 * p_node + 2] != 0)) {
            PreOrderTraverse(T, 2 * p_node + 2);
        }
    }
}

int main() {
    BiTree T = { 0 };
    InitBiTree(T);

    PreOrderTraverse(T,0);
    return 0;
}
/*
运行结果为：
按照层次从左往右输入树中结点的值，0 表示空结点，# 表示输入结束:1 2 3 4 5 6 7#
1 2 4 5 3 6 7
*/

对于链表存储的二叉树，递归实现先序遍历二叉树的 C 语言代码为:

#include <stdio.h>
#include <stdlib.h>
#define TElemType int

typedef struct BiTNode {
    TElemType data;//数据域
    struct BiTNode* lchild, * rchild;//左右孩子指针
}BiTNode, * BiTree;

void CreateBiTree(BiTree* T) {
    int num;
    scanf("%d", &num);
    //如果输入的值为 0，表示无此结点
    if (num == 0) {
        *T = NULL;
    }
    else
    {
        //创建新结点
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = num;
        CreateBiTree(&((*T)->lchild));//创建该结点的左孩子
        CreateBiTree(&((*T)->rchild));//创建该结点的右孩子
    }
}

void PreOrderTraverse(BiTree T) {
    //如果二叉树存在，则遍历二叉树
    if (T) {
        printf("%d ", T->data); //调用操作结点数据的函数方法
        PreOrderTraverse(T->lchild);//访问该结点的左孩子
        PreOrderTraverse(T->rchild);//访问该结点的右孩子
    }
}

//后序遍历二叉树，释放树占用的内存
void DestroyBiTree(BiTree T) {
    if (T) {
        DestroyBiTree(T->lchild);//销毁左孩子
        DestroyBiTree(T->rchild);//销毁右孩子
        free(T);//释放结点占用的内存
    }
}

int main() {
    BiTree Tree;
    CreateBiTree(&Tree);
    PreOrderTraverse(Tree);
    DestroyBiTree(Tree);
    return 0;
}
/*
运行结果为：
1 2 4 0 0 5 0 0 3 6 0 0 7 0 0
1 2 4 5 3 6 7
*/

中序遍历 #

二叉树的中序遍历，指的是从根结点出发，按照以下步骤访问二叉树中的每个结点：

先进入当前结点的左子树，以同样的步骤遍历左子树中的结点；
访问当前结点；
最后进入当前结点的右子树，以同样的步骤遍历右子树中的结点。

举个简单的例子，下图是一棵二叉树：

中序遍历这棵二叉树的过程是：

进入结点 A 的左子树，访问左子树中的结点；
    进入结点 B 的左子树，访问左子树中的结点；
        试图进入结点 D 的左子树，但该结点没有左子树；
        访问结点 D；
        试图进入结点 D 的右子树，但该结点没有右子树；
    访问结点 B；
    进入结点 B 的右子树，访问右子树中的结点；
        试图进入结点 E 的左子树，但该结点没有左子树；
        访问结点 E；
        试图进入结点 E 的右子树，但该结点没有右子树；
访问结点 A；
进入结点 A 的右子树，访问右子树中的结点；
    进入结点 C 的左子树，访问左子树中的结点；
        试图进入结点 F 的左子树，但该结点没有左子树；
        访问结点 F；
        试图进入结点 F 的右子树，但该结点没有右子树；
    访问结点 C；
    进入结点 C 的右子树，访问右子树中的结点；
        试图进入结点 G 的左子树，但该结点没有左子树；
        访问结点 G；
        试图进入结点 G 的右子树，但该结点没有右子树；

最终，中序遍历上图中的二叉树，访问各个结点的顺序是：
D B E A F C G

实现代码 #

对于顺序表存储的二叉树，递归实现中序遍历的 C 语言程序为：

#include <stdio.h>
#define NODENUM 7
#define ElemType int
//自定义 BiTree 类型，表示二叉树
typedef ElemType BiTree[NODENUM];

//存储二叉树
void InitBiTree(BiTree T) {
    ElemType node;
    int i = 0;
    printf("按照层次从左往右输入树中结点的值，0 表示空结点，# 表示输入结束:");
    while (scanf("%d", &node))
    {
        T[i] = node;
        i++;
    }
}

void INOrderTraverse(BiTree T, int p) {
    //递归遍历左子树
    if (((2 * p + 1) < NODENUM) && (T[2 * p + 1] != 0)) {
        INOrderTraverse(T, 2 * p + 1);
    }

    printf("%d ", T[p]);

    //递归遍历右子树
    if (((2 * p + 2) < NODENUM) && (T[2 * p + 2] != 0)){
        INOrderTraverse(T, 2 * p + 2);
    }  
}

int main() {
    BiTree T = { 0 };
    InitBiTree(T);

    INOrderTraverse(T, 0);

    return 0;
}
/*
执行结果为：
按照层次从左往右输入树中结点的值，0 表示空结点，# 表示输入结束:1 2 3 4 5 6 7 #
4 2 5 1 6 3 7
*/

对于链表存储的二叉树，递归实现中序遍历的 C 语言程序为：

#include <stdio.h>
#include <stdlib.h>
#define TElemType int

typedef struct BiTNode {
    TElemType data;//数据域
    struct BiTNode* lchild, * rchild;//左右孩子指针
}BiTNode, * BiTree;

void CreateBiTree(BiTree* T) {
    int num;
    scanf("%d", &num);
    //如果输入的值为 0，表示无此结点
    if (num == 0) {
        *T = NULL;
    }
    else
    {
        //创建新结点
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = num;
        CreateBiTree(&((*T)->lchild));//创建该结点的左孩子
        CreateBiTree(&((*T)->rchild));//创建该结点的右孩子
    }
}

//后序遍历二叉树，释放树占用的内存
void DestroyBiTree(BiTree T) {
    if (T) {
        DestroyBiTree(T->lchild);//销毁左孩子
        DestroyBiTree(T->rchild);//销毁右孩子
        free(T);//释放结点占用的内存
    }
}

void INOrderTraverse(BiTree T) {
    if (T) {
        INOrderTraverse(T->lchild);//遍历当前结点的左子树
        printf("%d ",T->data);     //访问当前结点
        INOrderTraverse(T->rchild);//遍历当前结点的右子树
    }
}

int main() {
    BiTree Tree;
    CreateBiTree(&Tree);
    INOrderTraverse(Tree);
    DestroyBiTree(Tree);
    return 0;
}
/*
运行结果：
1 2 4 0 0 5 0 0 3 6 0 0 7 0 0
4 2 5 1 6 3 7
*/

后序遍历 #

后序遍历二叉树，指的是从根结点出发，按照以下步骤访问树中的每个结点：

优先进入当前结点的左子树，以同样的步骤遍历左子树中的结点；
如果当前结点没有左子树，则进入它的右子树，以同样的步骤遍历右子树中的结点；
直到当前结点的左子树和右子树都遍历完后，才访问该结点。

以下图所示的二叉树为例：

后序遍历这棵二叉树的过程是：

从根节点 A 出发，进入该结点的左子树；
    进入结点 B 的左子树，遍历左子树中的结点：
        进入结点 D 的左子树，但该结点没有左孩子；
        进入结点 D 的右子树，但该结点没有右子树；
        访问结点 D；
    进入结点 B 的右子树，遍历右子树中的结点：
        进入结点 E 的左子树，但该结点没有左孩子；
        进入结点 E 的右子树，但该结点没有右孩子；
        访问结点 E；
    访问结点 B；
进入结点 A 的右子树，遍历右子树中的结点：
    进入结点 C 的左子树，遍历左子树中的结点：
        进入结点 F 的左子树，但该结点没有左孩子；
        进入结点 F 的右子树，但该结点没有右子树；
        访问结点 F；
    进入结点 C 的右子树，遍历右子树中的结点：
        进入结点 G 的左子树，但该结点没有左孩子；
        进入结点 G 的右子树，但该结点没有右孩子；
        访问结点 G；
    访问结点 C；
访问结点 A。

最终，后序遍历图 1 中的二叉树，访问各个结点的顺序是：
D E B F G C A

实现代码 #

后序遍历二叉树，最常用的实现方式就是递归。对于顺序表存储的二叉树，递归实现后序遍历的 C 语言程序为：

#include <stdio.h>
#define NODENUM 7
#define ElemType int
//自定义 BiTree 类型，表示二叉树
typedef ElemType BiTree[NODENUM];

//存储二叉树
void InitBiTree(BiTree T) {
    ElemType node;
    int i = 0;
    printf("按照层次从左往右输入树中结点的值，0 表示空结点，# 表示输入结束:");
    while (scanf("%d", &node))
    {
        T[i] = node;
        i++;
    }
}

//后序遍历二叉树
void PostOrderTraverse(BiTree T, int p) {
    if ((p * 2 + 1 < NODENUM) && (T[p * 2 + 1] != 0)) {
        PostOrderTraverse(T, 2 * p + 1);
    }
    if ((p * 2 + 2 < NODENUM) && (T[p * 2 + 2] != 0)) {
        PostOrderTraverse(T, 2 * p + 2);
    }
    printf("%d ", T[p]);
}

int main() {
    int res;
    BiTree T = { 0 };
    InitBiTree(T);
    PostOrderTraverse(T,0);
    return 0;
}
/*
* 运行结果为：
* 按照层次从左往右输入树中结点的值，0 表示空结点，# 表示输入结束:1 2 3 4 5 6 7 #
* 4 5 2 6 7 3 1
*/

对于链表存储的二叉树，递归实现后序遍历的 C 语言程序为：

#include <stdio.h>
#include <stdlib.h>
#define TElemType int

typedef struct BiTNode {
    TElemType data;//数据域
    struct BiTNode* lchild, * rchild;//左右孩子指针
}BiTNode, * BiTree;

void CreateBiTree(BiTree* T) {
    int num;
    scanf("%d", &num);
    //如果输入的值为 0，表示无此结点
    if (num == 0) {
        *T = NULL;
    }
    else
    {
        //创建新结点
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = num;
        CreateBiTree(&((*T)->lchild));//创建该结点的左孩子
        CreateBiTree(&((*T)->rchild));//创建该结点的右孩子
    }
}

//后序遍历
void PostOrderTraverse(BiTree T) {
    if (T) {
        PostOrderTraverse(T->lchild);//遍历左孩子
        PostOrderTraverse(T->rchild);//遍历右孩子
        printf("%d ", T->data);
    }
}

//后序遍历二叉树，释放树占用的内存
void DestroyBiTree(BiTree T) {
    if (T) {
        DestroyBiTree(T->lchild);//销毁左孩子
        DestroyBiTree(T->rchild);//销毁右孩子
        free(T);//释放结点占用的内存
    }
}

int main() {
    BiTree Tree;
    CreateBiTree(&Tree);
    PostOrderTraverse(Tree);
    DestroyBiTree(Tree);
    return 0;
}

/*
* 运行结果为：
* 1 2 4 0 0 5 0 0 3 6 0 0 7 0 0
* 4 5 2 6 7 3 1
*/

层序遍历 #

层序遍历很简单，就是按照层级进行遍历的，如下图所示，按照层序遍历结果很明显，第一层为1，第二层为2,3,第三层为4,5

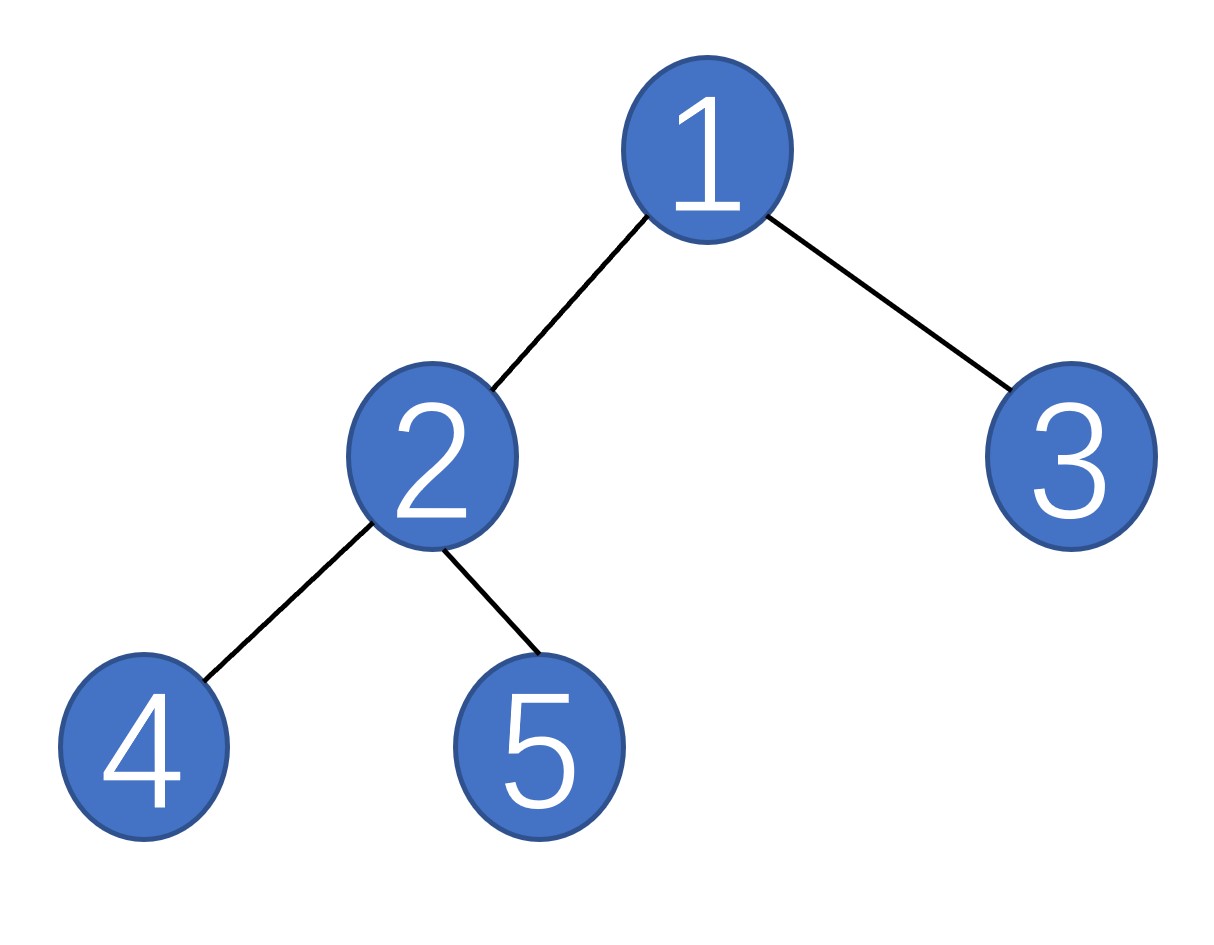
为了完成层序遍历，常需要辅助队列:

首先把根结点root放入队列中, 在搜索的每一轮中，记录下当前队列中包含的结点个数
从队列中依次取出结点，直到取出了上一层的全部结点为止，将结点值放入临时列表，再将子结点放入队列中
依次重复上述过程，直到遍历完成

实现代码 #

下面是层序遍历的迭代实现过程：

from collections import deque

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
    
tree = TreeNode(1, TreeNode(2), TreeNode(3))
tree.left.left = TreeNode(4)
tree.left.right = TreeNode(5)      

def levelOrder(root):
    levelOrder = list()
    if not root:
        return levelOrder
    q = deque([root])
    while q:
        level = list()
        size = len(q)
        for _ in range(size):
            node = q.popleft()
            level.append(node.val)
            if node.left:
                q.append(node.left)
            if node.right:
                q.append(node.right)
        levelOrder.append(level)

    return levelOrder[::1]

print(levelOrder(tree))

1 乐高STEAM

2 Scratch

3 Python

4 C++

5 创客

6 PPT创作

7 科创课题

8 关于我们

前序遍历 #

实现代码 #

中序遍历 #

实现代码 #

后序遍历 #

实现代码 #

层序遍历 #

实现代码 #

您的感觉是什么

前序遍历 #

实现代码 #

中序遍历 #

实现代码 #

后序遍历 #

实现代码 #

层序遍历 #

实现代码 #

您的感觉是什么

分享这篇文章 ：

分享这篇文章：