主要内容 #
- 波兰表达式
- 全排列问题
1. 波兰表达式 #
问题描述
波兰表达式是一种运算符置前的算数表达式,例如普通的表达式2+3的逆波兰表达式法为+2 3。波兰表达式的优点是运算符之下不必有优先级关系,也不必用括号改变运算次序,例如(2+3)*4的波兰表达式的表达法为*+2 3 4。本题求解波兰表达式的值,其中的运算符号包括“+”,“—”,“*”,“/”四个。
输入
一行,其中运算符号和运算数之间都用空格分隔,运算数是浮点数。
输出
一行,表达式的值。
样例输入
* + 11.0 12.0 + 24.0 35.0
样例输出
1357.000000
提示:(11.0+12.0)*(24.0+35.0)
算法原理 #
简单来说,这种表达式就是运算符号在全部在前面,需要运算的数值在后面,好像这种叫法是后缀表达式。
运算的原理是:从左往右走,如果某个运算符后面是连着2个数字的,那么计算其结果,然后再把其结果放在运算符的位置,参与运算的数移除,后面剩余的数字再往左移,依次类推,完成整个表达式的计算。
参考程序 #
#include < cstdio >
#include < cstring >
#include < algorithm >
using namespace std;
char str[101];
double hxs;
double exp(){
// 边读入数字边递归计算。
//以空格为分界读入数据
scanf("%s", str);
switch(str[0]){
//case 语句分情况处理
case '+' : hxs = exp() + exp(); break;
case '-' : hxs = exp() - exp(); break;
case '*' : hxs = exp() * exp(); break;
case '/' : hxs = exp() / exp(); break;
//使用atof(str)将字符串str转化为一个double类型的浮点数
default : hxs = atof(str);
}
return hxs;
}
int main(){
printf("%f\n",exp());
return 0;
}
2. 全排列问题 #
问题描述
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。
我们假设对于小写字母有a<b<···<y<z,而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入
只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度子在1~6之间。
输出
输出这个字符串所有的排列方式,每一行一个排列。要求字母序比较小的排在前面。
样例输入
abc
样例输出
abc
acb
bac
bca
cab
cba
算法原理 #
用字符串ans来存储排列结果,基本思想是递归地向数组ans[i]中放元素s[i],直到i==len-1时到达递归的边界从而输出结果。由于输入的字符串已经排序,只需按顺序选取结果自然是按照字典序排列。具体的递归过程见下图,图中1,2,3分别代表输入的三位字符。
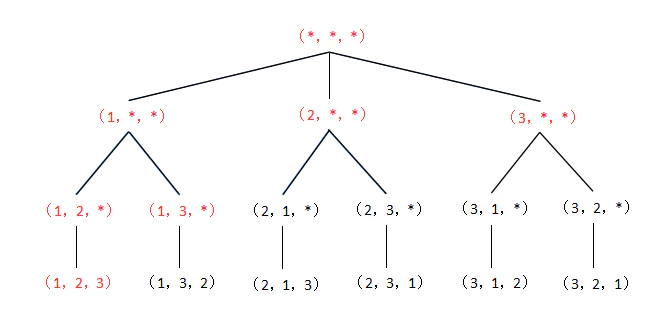
上图是一个树,树叶为解,即一个排列。从左至右,解按字典序出现。此树展示了逐步生成完整解的过程,这个过程具有横向循环,纵向递归的特点。横向循环表示每一步有多种选择,纵向递归表示每一步操作相似可以由递归来实现。具有这样特点的树叫解答树。解答树的结点数几乎全部由最后两层的结点数贡献,上面的结点数可忽略不计。此解答树的实现程序对应于程序1。
参考程序 #
#include < iostream >
#include < string >
#include < cstring >
using namespace std;
bool b[1001]; //b表示字母是否被选过。
char s[1001], ans[1001];
int len; //存储字符串的长度
void dfs(int i){
for(int j = 0; j < len; ++j){
if(!b[s[j]]) //判断是否重复
{
b[s[j]] = 1;
ans[i] = s[j];
if(i == len - 1){ // 达到长度后输出方案
cout << ans;
cout << endl;
}else{
dfs(i + 1); //搜索下一长度的方案
}
b[s[j]] = 0; //回溯法,退回上一长度重新搜索
}
}
}
int main(){
cin >> s;
len = strlen(s);
dfs(0);
return 0;
}



