主要内容 #

1. 上台阶问题
2. 平面分割问题

1.上台阶问题 #

问题描述 #

请思考以下问题，并动手编写程序：
楼梯有n个台阶，上楼可以一步上一个台阶，也可以一步上两个台阶。一共有多少种上楼的方法？

问题分析 #

1. 假设有1个台阶，只有1种方法：

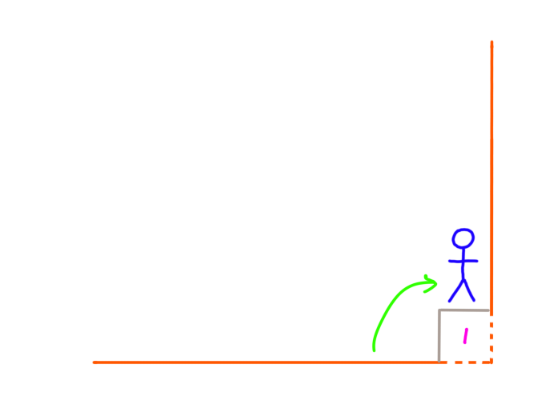
2. 假设有2级台阶，只有2种方法：


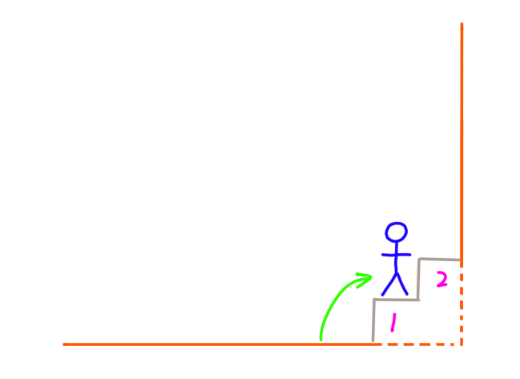
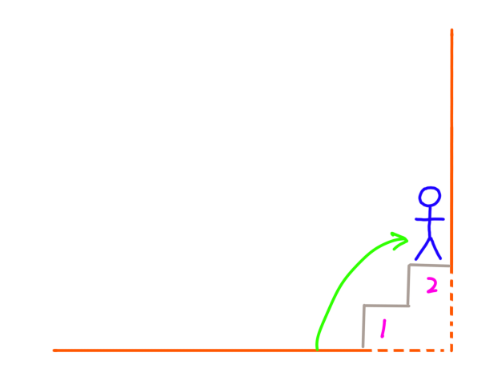
3. 假设有3级台阶
3.1 先爬1阶，接下来还有2阶台阶，那问题就是有2阶台阶怎么爬：

3.2 先爬2阶，接下来还有1阶台阶，那问题就是有1阶台阶怎么爬：

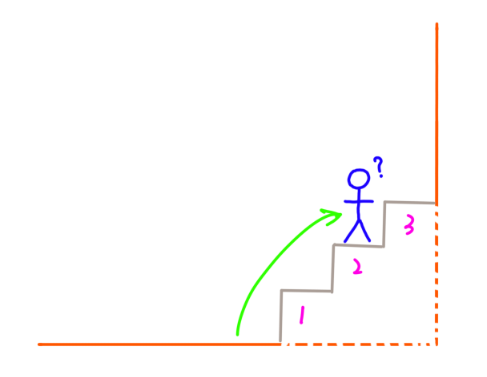
4. 假设有n级台阶
4.1 先爬1阶，接下来还有 n – 1 阶台阶，那问题就是有n – 1阶台阶怎么爬:

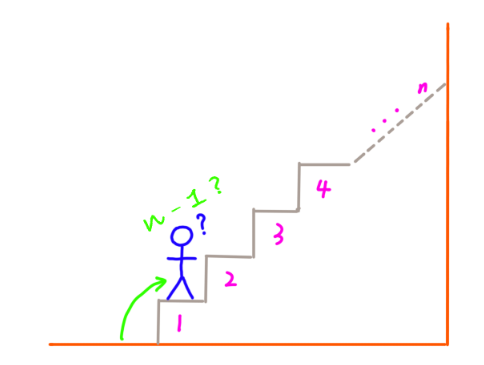
4.2 先爬2阶，接下来还有 n – 2 阶台阶，那问题就是有n – 2阶台阶怎么爬：

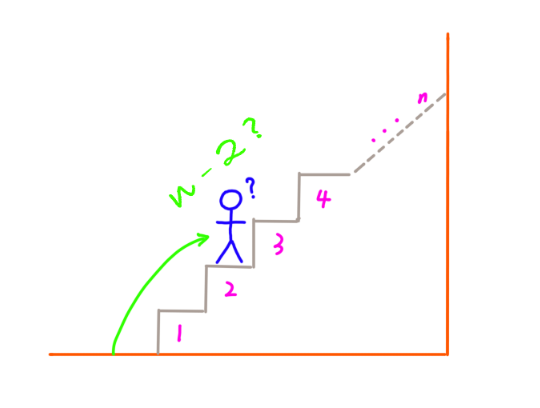
数学归纳法得出，有n阶台阶那么就是 n – 1 阶台阶和 n – 2 阶台阶爬上楼顶的方法的和。
公式： f(n) = f(n – 1) + f(n – 2) , 这不就是菲波那切数列数量求和吗？

编程求解 #

#include < iostream >
#include < vector >
using namespace std;
int climbStairs(int n) {
   //建立容器
   vector dp(n+1, 0);
   //设定边界值
   dp[0]=1;
   dp[1]=1;
   //循环求解
   for(int i=2;i<=n;i++){
      dp[i]=dp[i-1]+dp[i-2];
   }
   return dp[n];
   }
int main(){
   int n;
   cin >> n;
   cout << climbStairs(n) << endl;
   return 0;
}

算法优化
使用容器占用较大的空间，可以用p,q,r三个变量循环代替容器。

#include < iostream >
using namespace std;
int climbStairs(int n) {
   int p = 0, q = 0, r = 1;
      for (int i = 1; i <= n; ++i) {
         p = q; 
         q = r; 
         r = p + q;
      }
      return r;
    }

int main(){
   int n;
   cin >> n;
   cout << climbStairs(n) << endl;
   return 0;
}