主要内容 #
- 算法的概念
- 算法的特点
- 时间复杂度和空间复杂度
1. 算法的概念 #
算法(algorithm),在数学和计算机科学之中,指一个被定义好的、计算机可施行其指示的有限步骤或次序,常用于计算、数据处理(Data processing)和自动推理。算法是有效方法(Effective method),包含一系列定义清晰的指令,并可于有限的时间及空间内清楚的表述出来。
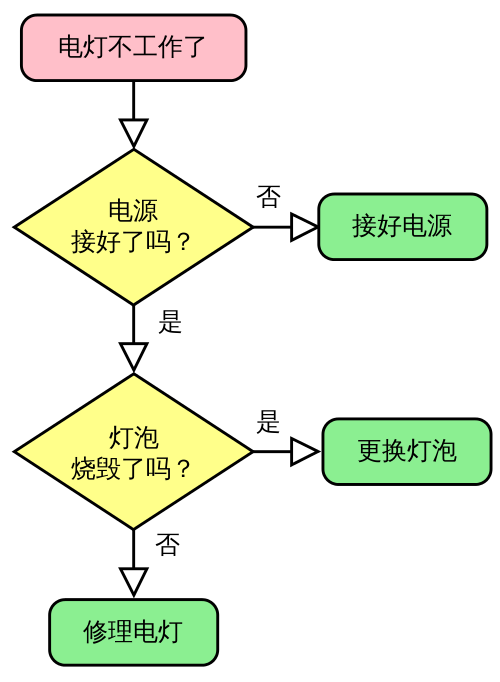
图1 应对灯泡不亮的简单算法流程图
简而言之,算法就是用来解决一个特定任务的一系列步骤。
2. 算法的特征 #
以下是高德纳在他的著作《计算机程序设计艺术》里对算法的特征进行的归纳:
a 输入:一个算法必须有零个或以上输入量。
b 输出:一个算法应有一个或以上输出量,输出量是算法计算的结果。
c 明确性:算法的描述必须无歧义,以保证算法的实际执行结果是精确地符合要求或期望,通常要求实际执行结果是确定的。
d 有限性:依据图灵的定义,一个算法是能够被任何图灵完备系统模拟的一串运算,而图灵机只有有限个状态、有限个输入符号和有限个转移函数(指令)。而一些定义更规定算法必须在有限个步骤内完成任务。
e 有效性:又称可行性。能够实现,算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。
3. 时间复杂度和空间复杂度 #
时间复杂度
算法的[[时间复杂度]]是指算法需要消耗的时间资源。一般来说,计算机算法是问题规模n的函数f(n),算法的时间复杂度也因此记做:T(n)= O(f(n))
常见的时间复杂度有:常数阶O(1),对数阶O(\log n),线性阶O(n),线性对数阶O(n\log n),平方阶O(n^2),立方阶O(n^3),…,k次方阶O(n^k),指数阶O(2^n)。随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
空间复杂度
算法的空间复杂度是指算法需要消耗的空间资源。其计算和表示方法与时间复杂度类似,一般都用复杂度的渐近性来表示。同时间复杂度相比,空间复杂度的分析要简单得多。



