主要内容 #

1. 枚举法的定义
2. 枚举法的计算步骤
3. 举例

1. 枚举法的定义 #

在进行归纳推理时，如果逐个考察了某类事件的所有可能情况，因而得出一般结论，那么该结论是可靠的，这种归纳方法叫做枚举法。由此可知，使用该算法需要满足两个条件：(1)可预先确定候选答案的数量；(2)候选答案的范围在求解之前必须有一个确定的集合。枚举在日常生活中很常见，例如“星期”这个词就是一个枚举，星期一、星期二、 星期三、星期四、星期五、星期六、星期日就是这个枚举里面的成员。
枚举算法的思想是：
将问题的所有可能的答案一一列举，然后根据条件判断此答案是否合适，保留合适的，舍弃不合适的。

2. 枚举法的计算步骤 #

枚举算法简单粗暴，他暴力的枚举所有可能，尽可能地尝试所有的方法。虽然枚举算法非常暴力，而且速度可能很慢，但确实我们最应该优先考虑的！因为枚举法变成实现最简单，并且得到的结果总是正确的。其计算步骤为：
（1）确定解题的可能范围，不能遗漏任何一个真正解，同时避免重复。
（2）判定是否是真正解的方法。
（3）为了提高解决问题的效率，使可能解的范围将至最小。

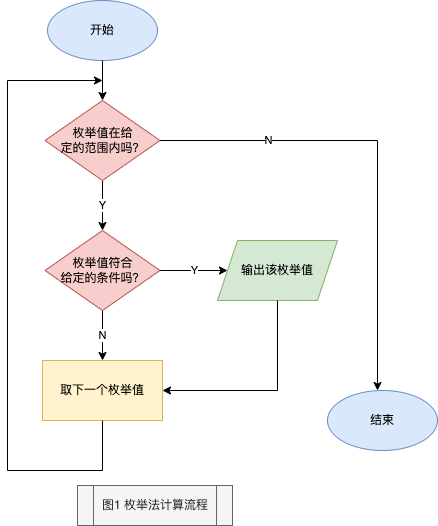
3. 举例 #

问题描述：
公鸡每只5元，母鸡每只3元，三只小鸡1元，用100元买100只鸡，问公鸡、母鸡、小鸡各多少只？
算法分析：
利用枚举法解决该问题，以三种鸡的个数为枚举对象,分别设为mj,gj和xj，用三种鸡的总数 （mj+gj+xj=100）和买鸡钱的总数（1/3*xj+mj*3+gj*5=100）作为判定条件，穷举各种鸡的个数。
参考程序：

#include<iostream>
using namespace std;
int main()
{
	int mj=0, gj=0, xj=0;                  //定义变量分别表示母鸡、公鸡、小鸡并初始化
	for (gj = 0; gj <= 20; gj++)		   //公鸡最多可买20个
	{
		for (mj = 0; mj <= 33; mj++)	   //母鸡最多可买33个
		{
			xj = 100 - gj - mj;			   // 三种鸡的总数是100只
			if (xj % 3 == 0 && 5 * gj + 3 * mj + xj / 3 == 100)// 总花费为100元
		    printf("公鸡为 %d 只，母鸡为 %d 只，小鸡为 %d 只！\n", gj, mj, xj);
		}
	}
	return 0;
}