主要内容 #
- 何为排序
- 排序的稳定性
- 排序的时间复杂度
- 排序的空间复杂度
1. 何为排序 #
排序是我们生活中经常遇到的问题,同学们出操的时候会按照从矮到高排列;老师查看上课出勤情况时,会按照学生的学号顺序点名;高考录取时会按照学生总分降序录取。这些都涉及到排序的概念。
排序的依据可以有不同种类,这种依据被称为关键字。如图所示,某学校为了选拔在主科上更为优秀的学生,要求对所有学生科目总分降序排列,并且在总分相同的情况下对语数外总分做降序排名,这里的总成绩就是主关键字,而语数外的总成绩是次关键字。
排序前:
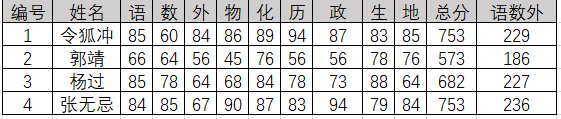
排序后:
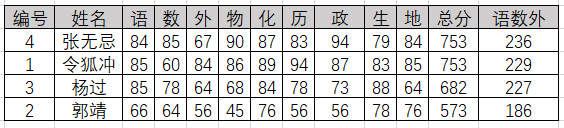
2. 排序的稳定性 #
也正是由于排序不仅是针对主关键字,那么对于此关键字,因为待排序的
记录序列中可能存在两个或者两个以上的关键字相等的记录,排序结果可能存在不唯一的情况,我们给出了稳定与不稳定的定义:
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
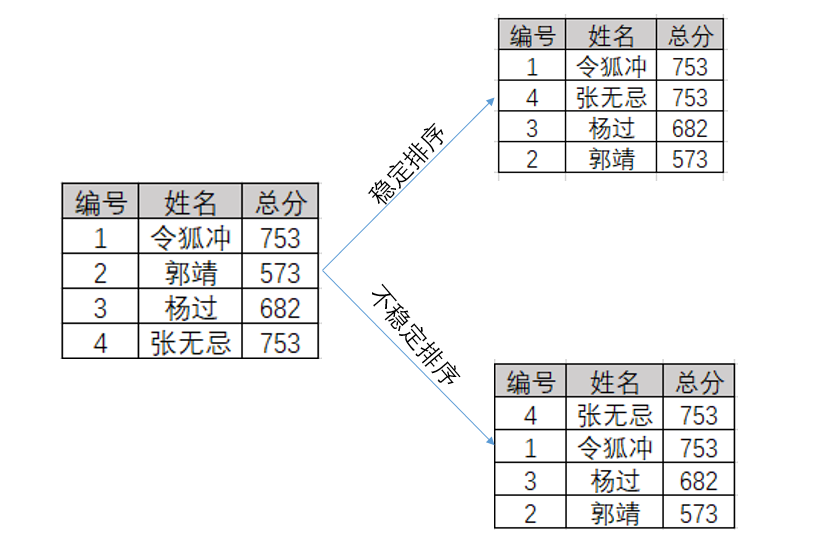
如下图所示:经过对总分排序后,总分高的排在前列。此时对于令狐冲和张无忌而言,未排序时时张无忌在前,那么它们总分排序后,分数相等的令狐冲依然在前,这样才算是稳定排序,如果他们二者颠倒了,此排序就是不稳定的了。
2. 排序的时间复杂度 #
排序是数据处理中经常执行的一种操作,往往属于系统的核心部分,因此排序算法的时间开销是衡量其好坏的重要标志。在内排序中,主要进行两种操作:比较和移动。比较是指关键字之间的比较,这是要做排序最起码的操作。移动是指记录从一个位置移动到另一个位置,高效的排序算法应该尽量减少关键字比较和记录的移动次数。
O ( 1 ) , O ( n ) , O ( l o g n ) , O ( n l o g n ) O(1), O(n), O(logn), O(nlogn)O(1),O(n),O(logn),O(nlogn)可以看作既可表示算法复杂度,也可以表示时间复杂度。
O后面的括号中有一个函数,指明某个算法的耗时/耗空间与数据增长量之间的关系。其中的n代表输入数据的量。
比如时间复杂度为O(n),就代表数据量增大几倍,耗时也增大几倍。比如常见的遍历算法。
再比如时间复杂度O(n^2),就代表数据量增大n倍时,耗时增大n的平方倍,这是比线性更高的时间复杂度。比如冒泡排序,就是典型的O(n^2)的算法,对n个数排序,需要扫描n×n次。
再比如O(logn),当数据增大n倍时,耗时增大logn倍(这里的log是以2为底的,比如,当数据增大256倍时,耗时只增大8倍,是比线性还要低的时间复杂度)。二分查找就是O(logn)的算法,每找一次排除一半的可能,256个数据中查找只要找8次就可以找到目标。
O(nlogn)同理,就是n乘以logn,当数据增大256倍时,耗时增大256*8=2048倍。这个复杂度高于线性低于平方。归并排序就是O(nlogn)的时间复杂度。
O(1)就是最低的时空复杂度了,也就是耗时/耗空间与输入数据大小无关,无论输入数据增大多少倍,耗时/耗空间都不变。 哈希算法就是典型的O(1)时间复杂度,无论数据规模多大,都可以在一次计算后找到目标(不考虑冲突的话)
3. 排序的空间复杂度 #
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。
冒泡排序,简单选择排序,堆排序,直接插入排序,希尔排序的空间复杂度为O(1),因为需要一个临时变量来交换元素位置,(另外遍历序列时自然少不了用一个变量来做索引)
快速排序空间复杂度为logn(因为递归调用了) ,归并排序空间复杂是O(n),需要一个大小为n的临时数组。



