跳至正文
View Categories

< 1 min read

主要内容 #

  1. 二分查找的概念
  2. 举例说明
  3. 二分法的特点

1. 二分查找的概念 #

二分查找（binary search）又叫做折半查找，它的要求是线性表中的数据必须是关键码有序的，线性表必须采用顺序存储。二分法的的关键思想是：在有序表中取中间值作为比较对象，若给定值与中间值相等则查找成功；若给定值比中间值小则在中间记录的左半区间（假设从小到大有序）查找；若给定值大于中间值；则在中间记录的右半区间查找。不断重复上述过程直到查找成功，或所有查找区域无记录，查找失败为止。
假设有这样一个有序数组{0,1,16,24,35,47,59,62,73,88,99}，除0下标外共有10个数字。对它进行查找是否存在62这个数字。可以看看折半算法是如何工作的

2. 二分查找的概念 #

/*二分查找*/
int Binary_Search(int *a, int n, int key){
    int low, high, mid;
    low = 1;    //定义最低下标为记录首位
    high = n;   //定义最高下标为记录末位
    while(low <= high){
        mid = (low + high) / 2  //折半
        if(key < a[mid])       //若查找值比中间值小
            high = mid - 1;     //最高下标调整到中位下标小一位
        else if(key > a[mid])  //若查找值比中间值大
            low = mid + 1;
        else 
            return mid;       //若相等则说明mid即为要查找的位置
    }
    return 0;
}

1. 程序运行开始，参数a={0,1,16,24,35,47,59,62,73,88,99}，n=10, key=62,第3～5行，此时low=1， high=10, 如下图所示：

2. 第6～15行循环，进行查找。
3. 第8行，mid计算得到5，由于a[5]=47<key，所以执行了第12行，low=5+1=6a，如下图所示：

4. 再次循环，mid=(6+10)/2=8，此时a[8]=73>key，所以执行第10行。high=8-1=7,如下图所示：

5. 再次循环，mid=(6+7)/2=6，此时a[8]=59<key，所以执行第12行，low=6+1=7，如下图所示：

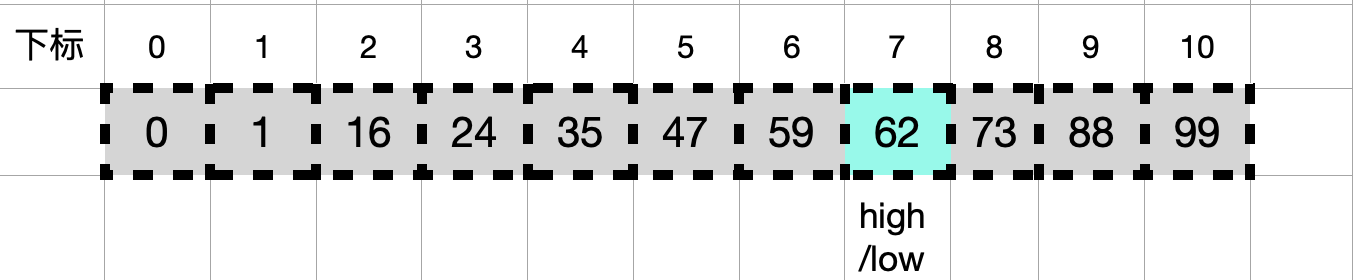
6. 再次循环，mid=(7+7)/2=7，此时a[8]=62=key，查找成功，返回7。

3. 二分法的特点 #

该算法还是挺容易理解的，同时也能感觉到它的效率非常高。到底有多高呢？关键在于该算法的时间复杂度。
首先将查找过程绘制成一棵二叉树，如下图所示，从图中就可以理解，如果查找的关键字不是中间记录47的话，二分法相当于把有序表分成了两棵子树，查找结果只需要找其中一半的数据即可，等于工作量减少了一半，然后继续二分查找，效率当然非常高了。

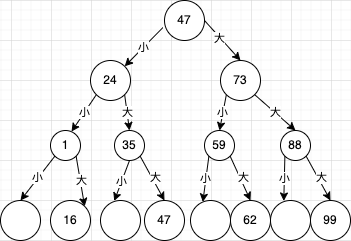
根据二叉树的特点，最坏的情况查找到关键字或者查找失败的次数为[log2n]+1。最好的情况当然是一次就找到了。
最终二分法的时间复杂度为O(logn)，显然要远优于顺序查找的O(n)时间复杂度了。
不过由于二分查找的前提条件是需要数据有序存储，对于频繁进行插入或者删除操作的数据集来说，维护有序排序会带来不小的工作量，不建议使用。

What are your Feelings