主要内容 #
- 第一个和最后一个位置
- 求解思路
- 参考代码
1. 第一个和最后一个位置 #
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例1
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]
示例2
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
示例3
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
2. 求解思路 #
1. 由于题目告知这个数组是升序排列的,所以可以通过二分查找的方法来解答此题;
2. 如何查找元素的第一个位置?利用二分查找找到数组中某元素值等于目标值 target 时,不像二分查找的模板那样立即返回(数组中有多个元素值等于 target),而是通过缩小查找区间的上边界 high (令high= mid – 1),不断向 mid 的左侧收缩,最后达到锁定左边界(元素的第一个位置)的目的;
3. 如何查找元素的最后一个位置?同查找元素的第一个位置类似,在查找到数组中某元素值等于目标值 target 时,不立即返回,通过增大查找区间的下边界 low (令low= mid + 1),不断向 mid 的右侧收缩,最后达到锁定右边界(元素的最后一个位置)的目的;
4. 没有找到,则直接返回 [-1,-1]。
以 nums = [5,7,7,8,8,10], target = 8 为栗子,通过下图来找出目标值 8 在数组中出现的第一个和最后一个位置。如下图示:
查找 8 出现的第一个位置:
由于此时 nums[mid] = 7 < target = 8,所以需要在右半区间 (mid, high] 中查找,即 low = mid + 1 = 3, mid = (high + low) /2 = 4。
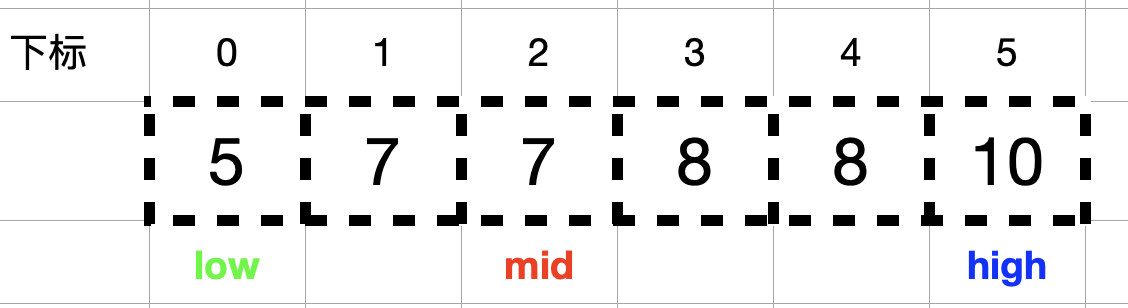
此时nums[mid] = 8 == target = 8, 按照解题思路方法一中 2 的描述,找到数组中元素值等于目标值 target 时,不立即返回,而是缩小查找区间的上边界 high (令 high = mid – 1 = 3),不断向 mid 的左侧收缩, mid = (high + low) / 2 = 3。
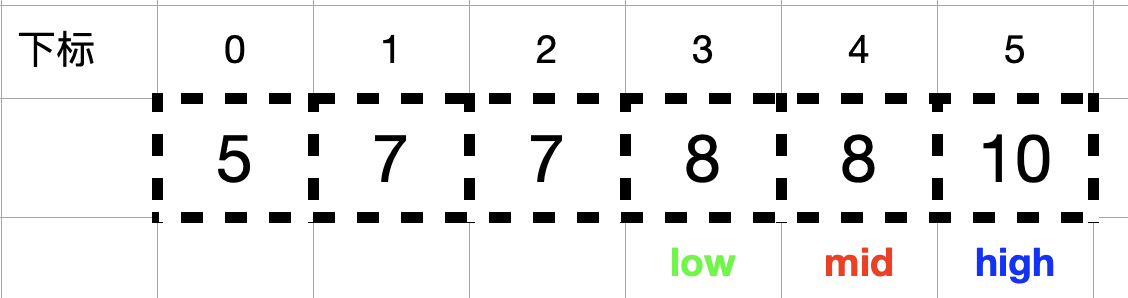
继续缩小查找区间的上边界 high。
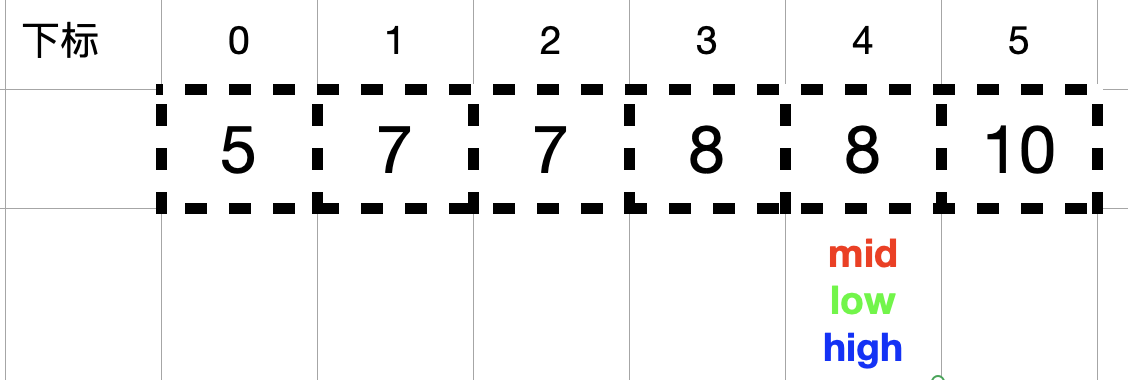
由于此时 high < low,代表查找 8 在数组中出现的第一个位置结束。
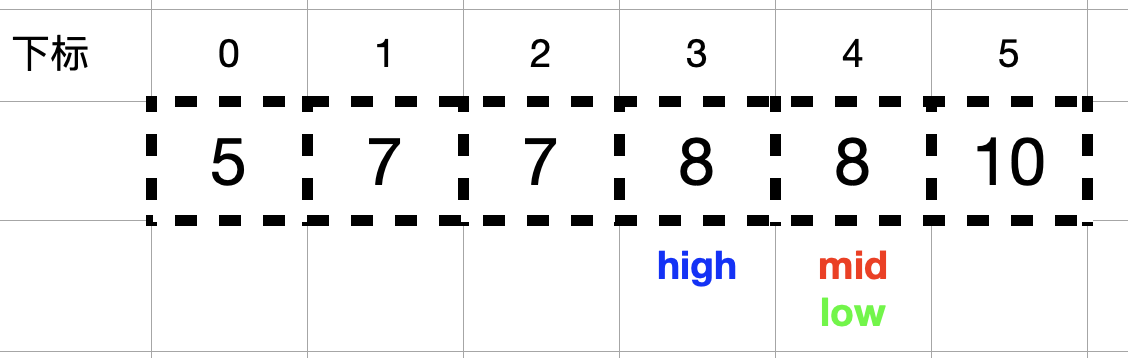
查找 8 出现的最后一个位置:
前两步跟查找 8 出现的第一个位置一样。
此时nums[mid] = 8 == target = 8, 按照解题思路方法一中 3 的描述,找到数组中元素值等于目标值 target 时,不立即返回,而是增大查找区间的下边界 low (令 low = mid + 1 = 5),不断向 mid 的右侧收缩,mid = (high + low) / 2 = 5。

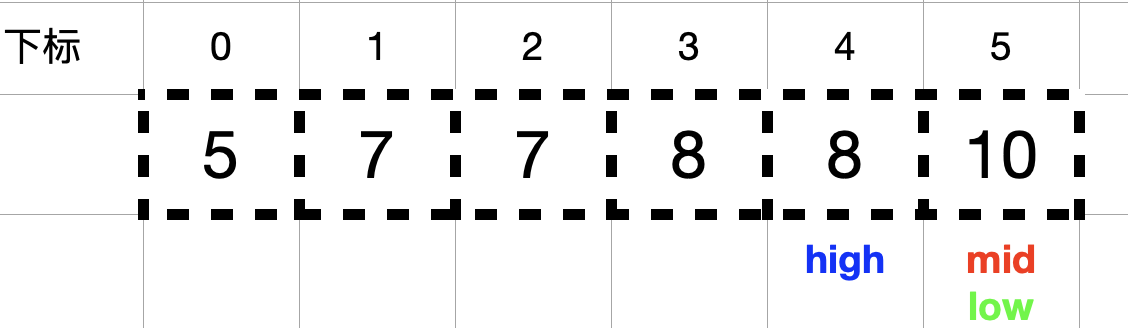
此时,nums[mid] = 10 > target = 8,high = mid – 1 = 4 。
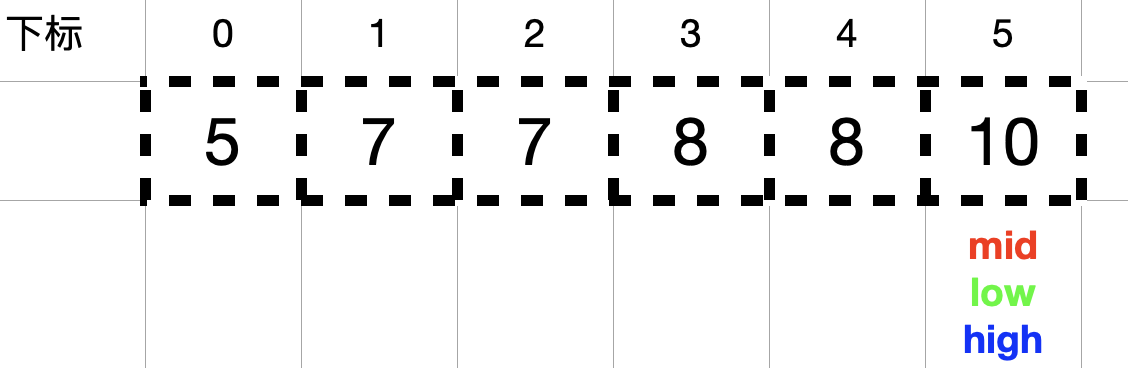
由于此时 high = 4 < low = 5,结束查找,代表查找 8 在数组中出现的最后一个位置结束。
3. 参考代码 #
int GetTargetPosition(int* nums, int numsSize, int target, int locFlag) {
int last = -1;
int low = 0, high = numsSize - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (nums[mid] < target) {
low = mid + 1;
} else if (nums[mid] > target) {
high = mid - 1;
} else if (nums[mid] == target) {
last = mid;
if (locFlag == 0) {
high = mid - 1;
} else {
low = mid + 1;
}
}
}
return last ;
}
int* searchRange(int* nums, int numsSize, int target, int* returnSize){
int* res = (int *)malloc(2 * sizeof(int));
memset(res, -1, 2 * sizeof(int));
*returnSize = 2;
if (nums == NULL || numsSize < 1) {
return res;
}
/* 通过 locFlag 标志区分查找的元素的位置在一个还是最后一个 */
int firstPos = GetTargetPosition(nums, numsSize, target, 0);
int lastPos = GetTargetPosition(nums, numsSize, target, 1);
/* 数组中没有目标元素 */
if (firstPos == -1 || lastPos == -1) {
return res;
}
res[0] = firstPos;
res[1] = lastPos;
return res;
}



