主要内容 #

1. 搜索旋转排序数组II
2. 搜索二维矩阵II

1. 搜索旋转排序数组II #

1.1题目描述 #

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。
示例：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true
输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

1.2求解思路 #

本篇题解基于第153讲，请读者在阅读完该题解后再继续阅读本篇题解。
对于数组中有重复元素的情况，二分查找时可能会有 a[l]=a[mid]=a[r]，此时无法判断区间 [l,mid] 和区间 [mid+1,r] 哪个是有序的。
例如nums=[3,1,2,3,3,3,3]，target=2，首次二分时无法判断区间[0,3] 和区间[4,6] 哪个是有序的。
对于这种情况，我们只能将当前二分区间的左边界加一，右边界减一，然后在新区间上继续二分查找。

1.3参考代码 #

class Solution {
public:
    bool search(vector<int> &nums, int target) {
        int n = nums.size();
        if (n == 0) {
            return false;
        }
        if (n == 1) {
            return nums[0] == target;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) {
                return true;
            }
            if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
                ++l;
                --r;
            } else if (nums[l] <= nums[mid]) {
                if (nums[l] <= target && target < nums[mid]) {
                    r = mid - 1;
                } else {
                    l = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return false;
    }
};

2. 搜索二维矩阵II #

2.1题目描述 #

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

2.2二分法求解 #

由于矩阵 matrix 中每一行的元素都是升序排列的，因此我们可以对每一行都使用一次二分查找，判断target 是否在该行中，从而判断 target 是否出现。
参考代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        for (int i = 0; i < m; i++) {
            int l = 0, r = n - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (matrix[i][mid] <= target) l = mid;
                else r = mid - 1;
            }
            if (matrix[i][r] == target) return true;
        }
        return false;
    }
};

复杂度分析
间复杂度O(mlogn)。对一行使用二分查找的时间复杂度为O(logn)，最多需要进行 mm 次二分查找。
空间复杂度：O(1)。

2.3单调性扫描法求解 #

在m x n矩阵 matrix中我们可以发现一个性质：对于每个子矩阵右上角的数x，x左边的数都小于等于x，x下边的数都大于x，如下图所示：

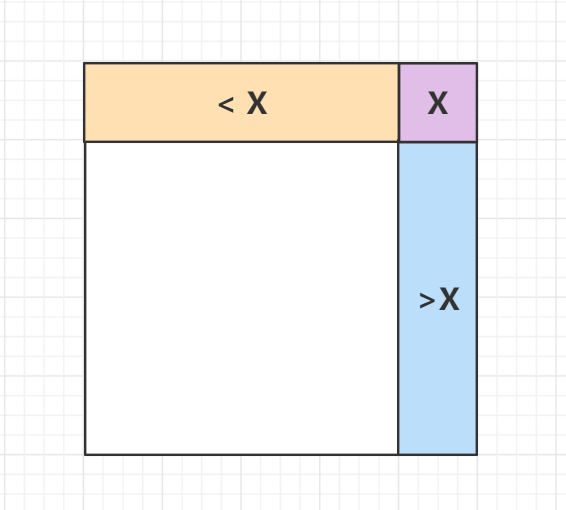
因此我们可以从整个矩阵的右上角开始枚举，假设当前枚举的数是 x：

• 如果 x 等于target，则说明我们找到了目标值，返回true；
• 如果 x小于target，则 x左边的数一定都小于target，我们可以直接排除当前一整行的数；
• 如果 x 大于target，则 x 下边的数一定都大于target，我们可以直接排除当前一整列的数；

排除一整行就是让枚举的点的横坐标加一，排除一整列就是让纵坐标减一。当我们排除完整个矩阵后仍没有找到目标值时，就说明目标值不存在，返回false。
参考代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(!matrix.size() && !matrix[0].size()) return false;
        int i = 0, j = matrix[0].size() - 1;  //矩阵右上角
        while(i < matrix.size() && j >= 0)
        {
            if(matrix[i][j] == target)  return true;
            else if( matrix[i][j] << target) i++;  //排除一行
            else if( matrix[i][j] > target) j--;  //排除一列
        }
        return false;
    }
};