主要内容 #

1. 动态规划的一般步骤
2. 连续最大子序列的和

1. 动态规划的一般步骤 #

动态规划是一种算法思路（注意这里不要和递归混淆， 事实上递归和迭代只是两种不同的实现方法， 并不是算法）， 用一句话来总结就是， 动态规划是利用存储历史信息使得未来需要历史信息时不需要重新计算，从而达到降低时间复杂度，用空间复杂度换取时间复杂度目的的方法。 动态规划分为以下几步：
（1）确定递推量。 这一步需要确定递推过程中要保留的历史信息数量和具体含义， 同时也会定下动态规划的维度；
（2）推导递推式。 根据确定的递推量， 得到如何利用存储的历史信息在有效时间（通常是常量或者线性时间）内得到当前的信息结果；
（3）计算初始条件。 有了递推式之后， 我们只需要计算初始条件， 就可以根据递推式得到我们想要的结果了。 通常初始条件都是比较简单的情况， 一般来说直接赋值即可；
（4）（可选）考虑存储历史信息的空间维度。这一步是基于对算法优化的考虑，一般来说几维动态规划我们就用几维的存储空间是肯定可以实现的。 但是有时我们对于历史信息的要求不高，比如这一步只需要用到上一步的历史信息，而不需要更早的了，那么我们可以只存储每一步的历史信息， 每步覆盖上一步的信息，这样便可以少一维的存储空间， 从而优化算法的空间复杂度。
动态规划的时间复杂度是O(（维度）×（每步获取当前值所用的时间复杂度））。基本上按照上面的思路，动态规划的题目都可以解决，不过最难的一般是在确定递推量，一个好的递推量可以使得动态规划的时间复杂度尽量低。

2. 连续最大子序列的和 #

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组是数组中的一个连续部分。

2.1 举例 #

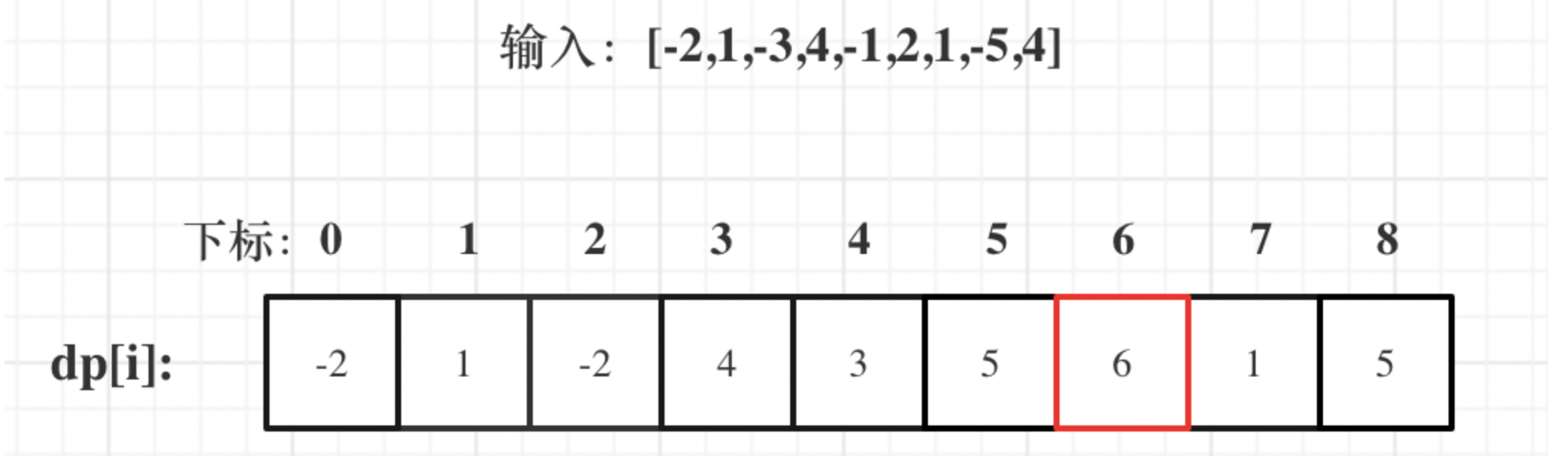
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: [4,-1,2,1] 最大的连续子串和sum = 6.

2.2 解题思路 #

1. 确定dp数组（dp table）以及下标的含义
dp[i]：包括下标i之前的最大连续子序列和为dp[i]。
2. 确定递推公式
dp[i]只有两个方向可以推出来：
dp[i – 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和
3. dp数组如何初始化
从递推公式可以看出来dp[i]是依赖于dp[i – 1]的状态，dp[0]就是递推公式的基础。
4. dp[0]应该是多少呢?
根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。
5. 确定遍历顺序
递推公式中dp[i]依赖于dp[i – 1]的状态，需要从前向后遍历。
举例推导dp数组：

2.3 参考代码 #

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        int result = dp[0];
        for (int i = 1; i < nums.size(); i++) {
            dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
            if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
        }
        return result;
    }
};