主要内容 #

1. 最长回文子序列
2. 求解思路
3. 参考代码

1. 最长回文子序列 #

给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1: 输入: “bbbab” 输出: 4 一个可能的最长回文子序列为 “bbbb”。
示例 2: 输入:”cbbd” 输出: 2 一个可能的最长回文子序列为 “bb”。
提示：
1. 1 <= s.length <= 1000
2. s 只包含小写英文字母
刚刚做过了 动态规划：回文子串，求的是回文子串，而本题要求的是回文子序列， 要搞清楚这两者之间的区别。
回文子串是要连续的，回文子序列可不是连续的！ 回文子串，回文子序列都是动态规划经典题目。

2. 求解思路 #

1. 确定dp数组（dp table）以及下标的含义
dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2. 确定递推公式
在判断回文子串的题目中，关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j – 1] + 2;

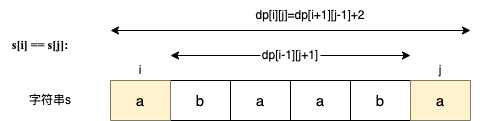
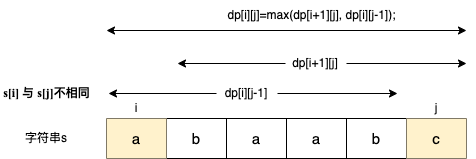
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j – 1]。
那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j – 1]);

代码如下：

if (s[i] == s[j]) {
    dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}

3. dp数组的初始化
首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j – 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j – 1]); 中dp[i][j]才不会被初始值覆盖。

vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;

4. 确定便利顺序
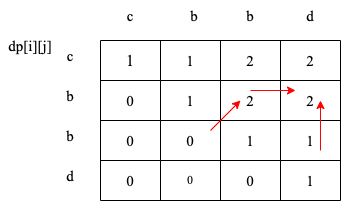
从递推公式dp[i][j] = dp[i + 1][j – 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j – 1]) 可以看出，dp[i][j]是依赖于dp[i + 1][j – 1] 和 dp[i + 1][j]，
也就是从矩阵的角度来说，dp[i][j] 下一行的数据。 所以遍历i的时候一定要从下到上遍历，这样才能保证，下一行的数据是经过计算的。
递推公式：dp[i][j] = dp[i + 1][j – 1] + 2，dp[i][j] = max(dp[i + 1][j], dp[i][j – 1]) 分别对应着下图中的红色箭头方向，如图：

代码如下：

for (int i = s.size() - 1; i >= 0; i--) {
    for (int j = i + 1; j < s.size(); j++) {
        if (s[i] == s[j]) {
            dp[i][j] = dp[i + 1][j - 1] + 2;
        } else {
            dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
}

5. 举例推导dp数组
输入s:”cbbd” 为例，dp数组状态如图：

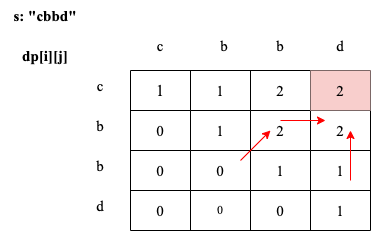
红色框即：dp[0][s.size() – 1]; 为最终结果。

3. 参考代码 #

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i + 1; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][s.size() - 1];
    }
};