主要内容 #

1. 问题描述
2. 求解思路
3. 参考代码

1. 问题描述 #

给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
如果链表中存在环 ，则返回 true 。 否则，返回 false 。

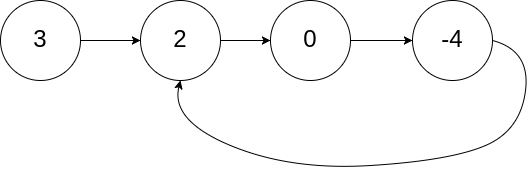
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

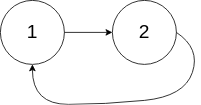
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

2. 求解思路 #

对于判断单向链表中是否存在环这个问题，我们可以先思考一下，如果存在环，那么当前链表会有什么特点？
存在环就说明链表的尾节点不是指向 null，而是指向了链表中的另一个节点，只有这样才会构成环，如下图所示就是一个存在环的单向链表：

我们设想一下这么个场景，比如说有两个人在圆形跑道上跑步，一个人一秒钟跑一米，另一个人一秒钟跑两米，然后他们两同时开始并且一直跑，那么他们会不会相遇呢？
答案是只要体力允许，他们两一定会在某一个点相遇；相反，如果是直线跑道，那么他们就不可能相遇。所以我们可以将这个思想利用起来，这就是快慢双指针法。
快慢双指针法主要步骤为：定义两个指针，一个 slow 指针，一次走一步；另一个 fast 指针，一次走两步。如果可以在某一个点满足 slow=fast，那么就说明存在环，否则 fast 指针必然先到到终点。

3. 参考代码 #

/*
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode* head) {
        if (head == nullptr || head->next == nullptr) { //注意这个条件，要防止空指针
            return false;
        }
        ListNode* slow = head;
        ListNode* fast = head->next;
        while (slow != fast) {
            if (fast == nullptr || fast->next == nullptr) {
                return false;
            }
            slow = slow->next;     //slow 指针一次一步
            fast = fast->next->next; //fast指针一次两步
        }
        return true;
    }
};