主要内容 #
- 树的定义
- 树的基本概念
- 树的其他表示方式
1. 树的定义 #
前面章节给大家介绍的都是线性存储结构,包括顺序表、链表、栈、队列、数组。从本节开始,带大家学习一种非线性存储结构,称为树存储结构。
树结构通常用来存储逻辑关系为 “一对多” 的数据。例如:
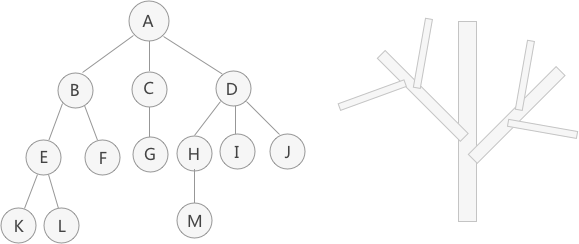
上图的这些元素具有的就是 “一对多” 的逻辑关系,例如元素 A 同时和 B、C、D 有关系,元素 D 同时和 A、H、I、J 有关系等。 观察这些元素之间的逻辑关系会发现,它们整体上很像一棵倒着的树上右图倒过来),这也是将存储它们的结构起名为“树”(或者 “树形”)的原因。
存储具有 “一对多” 逻辑关系的数据,数据结构推荐使用树存储结构。
2. 树的基本概念 #
就好像学习链表要知道 “结点” 代表什么意思。系统学习树存储结构之前,也必须了解一些相关的术语。
1) 结点
和链表类似,树存储结构中也将存储的各个元素称为 “结点”。例如在上图中,元素 A 就是一个结点。
对于树中某些特殊位置的结点,还可以进行更细致的划分,比如:
- 父结点(双亲结点)、孩子结点和兄弟结点:以上图中的结点 A、B、C、D 为例,A 是 B、C、D 结点的父结点(也称为“双亲结点”),而 B、C、D 都是 A 结点的孩子结点(也称“子结点”)。对于 B、C、D 来说,它们都有相同的父结点,所以它们互为兄弟结点;
- 树根结点(简称 “根结点” ):特指树中没有双亲(父亲)的结点,一棵树有且仅有一个根结点。例如上图中,结点 A 就是整棵树的根结点;
- 叶子结点(简称 “叶结点” ):特指树中没有孩子的结点,一棵树可以有多个叶子结点。例如上图中,结点 K、L、F、G、M、I、J 都是叶子结点。
2) 子树
仍以上图的树为例,A 是整棵树的根结点。但如果单看结点 B、E、F、K、L 组成的部分来说,它们也组成了一棵树,结点 B 是这棵树的根结点。通常,我们将一棵树中几个结点构成的“小树”称为这棵树的“子树”。
知道了子树的概念后,树也可以这样定义:树是由根结点和若干棵子树构成的。例如,上图这棵树就是由结点 A 和分别以 B、C、D 为根节点的子树构成。
注意:单个结点也可以看作是一棵树,该结点即为根结点。例如上图中,结点 K、L、F 各自就可以看作是一棵树,只不过树中只有一个根节点而已。
3) 结点的度
一个结点拥有子树的个数,就称为该结点的度(Degree)。例如上图中,根结点 A 有 3 个子树,它们的根节点分别是 B、C、D,因此结点 A 的度为 3。
比较一棵树中所有结点的度,最大的度即为整棵树的度。比如上图中,所有结点中最大的度为 3,所以整棵树的度就是 3。
4) 结点的层次
从一棵树的树根开始,树根所在层为第一层,根的孩子结点所在的层为第二层,依次类推。
对于上图这棵树来说,A 结点在第一层,B、C、D 为第二层,E、F、G、H、I、J 在第三层,K、L、M 在第四层。
树中结点层次的最大值,称为这棵树的深度或者高度。例如上图这棵树的深度为 4。
如果两个结点的父结点不同,但它们父结点的层次相同,那么这两个结点互为堂兄弟。例如上图中,结点 G 和 E、F、H、I、J 的父结点都在第二层,所以它们互为堂兄弟。
5) 有序树和无序树
如果一棵树中,各个结点左子树和右子树的位置不能交换,那么这棵树就称为有序树。反之,如果树中结点的左、右子树可以互换,那么这棵树就是一棵无序树。
在有序树中,结点最左边的子树称为 “第一个孩子”,最右边的称为 “最后一个孩子”。拿上图这棵树来说,如果它是一棵有序树,那么以结点 B 为根结点的子树为整棵树的第一个孩子,以结点 D 为根结点的子树为整棵树的最后一个孩子。
6) 森林
由 m(m >= 0)个互不相交的树组成的集合就称为森林。比如上图中除去 A 结点,那么分别以 B、C、D 为根结点的三棵子树就可以称为森林。
前面讲到,树可以理解为是由根结点和若干子树构成的,而这若干子树本身就是一个森林,因此树还可以理解为是由根结点和森林组成的。
7) 空树(简单了解即可)
空树指的是没有任何结点的树,连根结点都没有。
3. 树的其他表示方式 #
除了上图这样画一棵树之外,还有其它的方式可以表示一棵树。

上图左侧是以嵌套集合的形式表示的(集合之间绝不能相交,即任意两个圆圈不能有交集)。
上图右侧使用的是凹入表示法,最长条为根结点,相同长度的表示在同一层次。例如 B、C、D 长度相同,都为 A 的子结点,E 和 F 长度相同,为 B 的子结点,K 和 L 长度相同,为 E 的子结点,依此类推。



