主要内容 #
- 什么是父亲表示法
- 父亲表示法的优缺点
- 如何表示一棵树
1. 什么是父亲表示法 #
C++ 中的树的父亲表示法(Parent Representation)又称为双亲表示法,是一种使用数组来表示树的数据结构,其中数组的下标表示节点的编号,数组的元素表示该节点的父节点编号。
注意,根节点没有父节点(父节点又称为双亲节点),因此根节点记录父节点位置的变量通常置为 -1。
例如,采用双亲表示法存储下图的普通树:
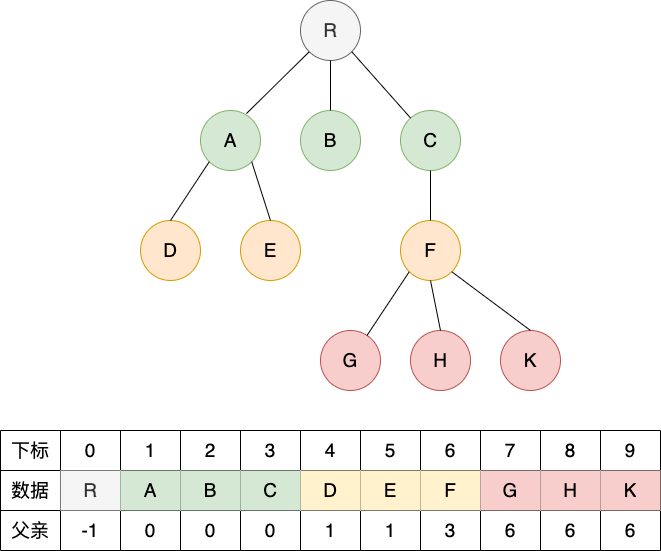
上图存储普通树的过程转化为 C 语言代码为:
#define MAX_SIZE 100//宏定义树中结点的最大数量
typedef char ElemType;//宏定义树结构中数据类型
typedef struct Snode{
TElemType data;//树中结点的数据类型
int parent;//结点的父结点在数组中的位置下标
}PTNode;
typedef struct {
PTNode tnode[MAX_SIZE];//存放树中所有结点
int n;//根的位置下标和结点数
}PTree;
2. 父亲表示法的优缺点 #
使用父亲表示法可以有效地节省存储空间,同时还能够支持一些特殊的树算法,如 LCA(最近公共祖先)等。但是需要注意,使用父亲表示法表示一棵树时,不支持快速查找某个节点的子节点,需要进行线性遍历。
但是,使用父亲表示法存储一棵树也存在一些缺点,例如:
1. 插入、删除节点时需要更新父节点指针,而且需要保证更新完毕之后整棵树依然合法,否则会导致程序出错。
2. 在进行节点查找时,需要从根节点开始遍历整棵树才能找到目标节点,这样的时间复杂度是 $O(n)$ 的。
3. 父亲表示法并不支持高效的树的重构操作。当需要重构一棵树时,需要重新构建整棵树,而无法利用已有的部分信息来高效地进行重构。
因此,在实际应用中,应根据具体的需求来选择合适的树的表示方法。当需要高效地进行节点查找或树的重构操作时,可能需要使用其他的树的表示方法,如孩子表示法、邻接表等。
另外,需要注意的是,父亲表示法有一些限制和约束条件,如:
1. 父节点编号必须唯一。即每个节点的父节点编号不能相同,否则无法正确地表示树的结构。
2. 根节点的父节点编号必须为一个特定值。根节点没有父节点,因此需要为其指定一个特殊的父节点编号,通常为 $-1$ 或 $0$ 等。
3. 节点的编号必须连续。如果使用数组来存储节点信息,则节点的编号必须从 $1$ 开始连续编号,否则无法正确地使用数组来访问节点信息。
4. 树的深度不能太大。由于父亲表示法需要存储每个节点的父节点编号,因此树的深度不能太大,否则会占用过多的存储空间,导致程序出错。
3. 如何表示一棵树 #
存储上图中普通树的 C 语言实现代码为:
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 20
typedef char ElemType;//宏定义树结构中数据类型
typedef struct Snode //结点结构
{
ElemType data;
int parent;
}PNode;
typedef struct //树结构
{
PNode tnode[MAX_SIZE];
int n; //结点个数
}PTree;
PTree InitPNode(PTree tree)
{
int i, j;
char ch;
printf("请输出节点个数:\n");
scanf("%d", &(tree.n));
printf("请输入结点的值其双亲位于数组中的位置下标:\n");
for (i = 0; i < tree.n; i++)
{
getchar();
scanf("%c %d", &ch, &j);
tree.tnode[i].data = ch;
tree.tnode[i].parent = j;
}
return tree;
}
void FindParent(PTree tree)
{
char a;
int isfind = 0;
printf("请输入要查询的结点值:\n");
getchar();
scanf("%c", &a);
for (int i = 0; i < tree.n; i++) {
if (tree.tnode[i].data == a) {
isfind = 1;
int ad = tree.tnode[i].parent;
printf("%c的父节点为 %c,存储位置下标为 %d", a, tree.tnode[ad].data, ad);
break;
}
}
if (isfind == 0) {
printf("树中无此节点");
}
}
int main()
{
PTree tree;
for (int i = 0; i < MAX_SIZE; i++) {
tree.tnode[i].data = " ";
tree.tnode[i].parent = 0;
}
tree = InitPNode(tree);
FindParent(tree);
return 0;
}
程序运行示例:
请输出节点个数: 10 请输入结点的值其双亲位于数组中的位置下标: R -1 A 0 B 0 C 0 D 1 E 1 F 3 G 6 H 6 K 6 请输入要查询的结点值: C C的父节点为 R,存储位置下标为 0



