主要内容 #

1. 问题描述
2. 求解思路
3. 参考代码

1. 问题描述 #

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这棵二叉树。
示例1：

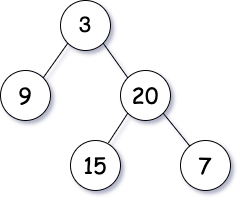
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
示例2：
输入：inorder = [-1], postorder = [-1]
输出：[-1]

2. 求解思路 #

首先来看题目给出的两个已知条件 中序遍历序列 和 后序遍历序列 根据这两种遍历的特性我们可以得出两个结论：

1. 在后序遍历序列中,最后一个元素为树的根节点
2. 在中序遍历序列中,根节点的左边为左子树，根节点的右边为右子树

树的还原过程描述：
根据中序遍历和后续遍历的特性我们进行树的还原过程分析

1. 首先在后序遍历序列中找到根节点(最后一个元素)
2. 根据根节点在中序遍历序列中找到根节点的位置
3. 根据根节点的位置将中序遍历序列分为左子树和右子树
4. 根据根节点的位置确定左子树和右子树在中序数组和后续数组中的左右边界位置
5. 递归构造左子树和右子树
6. 返回根节点结束

算法

• 为了高效查找根节点元素在中序遍历数组中的下标，我们选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表。
• 定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界，递归入口为helper(0, n – 1)：

1. 如果 in_left > in_right，说明子树为空，返回空节点。
2. 选择后序遍历的最后一个节点作为根节点。
3. 利用哈希表O(1) 查询当根节点在中序遍历中下标为 index。从 in_left 到 index – 1 属于左子树，从 index + 1 到 in_right 属于右子树。
4. 根据后序遍历逻辑，递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index – 1)。注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。
5. 返回根节点 root。

3. 参考代码 #

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    int post_idx;
    unordered_map<int, int> idx_map;
public:
    TreeNode* helper(int in_left, int in_right, vector<int>& inorder, vector<int>& postorder){
        // 如果这里没有节点构造二叉树了，就结束
        if (in_left > in_right) {
            return nullptr;
        }

        // 选择 post_idx 位置的元素作为当前子树根节点
        int root_val = postorder[post_idx];
        TreeNode* root = new TreeNode(root_val);

        // 根据 root 所在位置分成左右两棵子树
        int index = idx_map[root_val];

        // 下标减一
        post_idx--;
        // 构造右子树
        root->right = helper(index + 1, in_right, inorder, postorder);
        // 构造左子树
        root->left = helper(in_left, index - 1, inorder, postorder);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        // 从后序遍历的最后一个元素开始
        post_idx = (int)postorder.size() - 1;

        // 建立（元素，下标）键值对的哈希表
        int idx = 0;
        for (auto& val : inorder) {
            idx_map[val] = idx++;
        }
        return helper(0, (int)inorder.size() - 1, inorder, postorder);
    }
};