主要内容 #

1. 问题描述
2. 求解思路
3. 参考代码

1. 问题描述 #

给定一棵二叉树，编写一个有效的算法来检查它是否具有对称结构，即左右子树相互镜像。例如，以下是一些具有对称结构的二叉树：

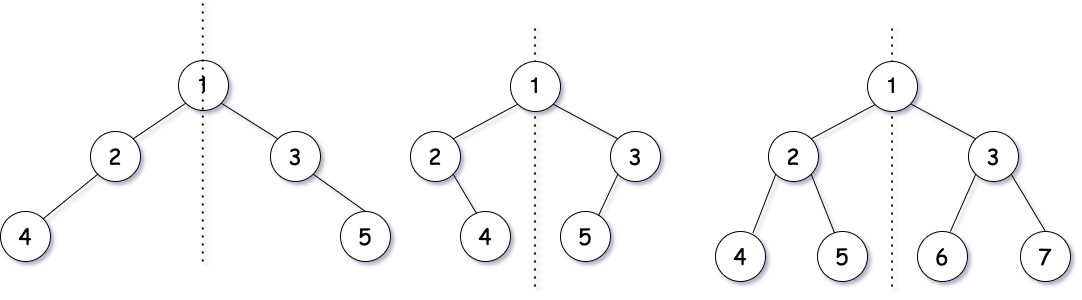
2. 求解思路 #

如果左右子树相互镜像，则该树具有对称结构。如果满足以下所有条件，则两棵树相互镜像：

• 两棵树都是空的，或者都是非空的。
• 左子树是右子树的镜像。
• 右子树是左子树的镜像。

我们可以使用递归快速检查这一点。

3. 参考代码 #

#include <iostream>
using namespace std;
 
// 存储二叉树节点的数据结构
struct Node
{
    int data;
    Node *left, *right;
 
    Node(int data)
    {
        this->data = data;
        this->left = this->right = nullptr;
    }
};
 
// 检查以 `X` 和 `Y` 为根的子树是否相互镜像的函数
bool isSymmetric(Node* X, Node* Y)
{
    // 基本情况：如果两棵树都是空的
    if (X == nullptr && Y == nullptr) {
        return true;
    }
 
    // 如果返回真
    // 1. 两棵树都是非空的，并且
    // 2. 左子树是右子树的镜像，并且
    // 3. 右子树是左子树的镜像
    return (X != nullptr && Y != nullptr) &&
        isSymmetric(X->left, Y->right) &&
        isSymmetric(X->right, Y->left);
}
 
// 检查给定二叉树是否具有对称结构的函数
bool isSymmetric(Node* root)
{
    // 基本情况
    if (root == nullptr) {
        return true;
    }
 
    // 如果左右子树相互镜像，则返回 true
    return isSymmetric(root->left, root->right);
}
 
int main()
{
    /* 构造下面的树
         1
       /  \
      /    \
     2      3
      \    /
       5  6
    */
 
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->right = new Node(4);
    root->right->left = new Node(5);
 
    if (isSymmetric(root)) {
        cout << "The binary tree is symmetric";
    }
    else {
        cout << "The binary tree is not symmetric";
    }
 
    return 0;
}