主要内容 #

1. 问题描述
2. 求解思路
3. 参考代码

1. 问题描述 #

输入一棵二叉树的根节点，求该树的深度。从根节点到叶子节点依次经过的节点（含根、叶子节点）形成树的一条路径，最长路径为树的深度。

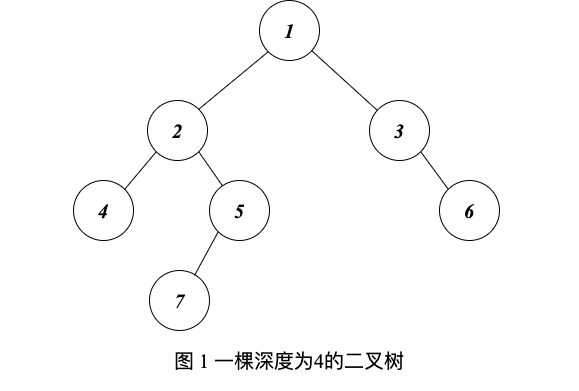
例如，在上图的二叉树深度为4，因为它从根节点到叶子节点最长路径包含4个节点（从根节点1开始，经过节点2和5，最终到达叶子节点7）。

2. 求解思路 #

我们从另一个角度来理解树的深度问题。
如果一棵树只有一个节点，那么它的深度是1。
如果根节点只有左子树而没有右子树没有右子树，那么树的深度就是左子树的深度加1。
同样，如果根节点只有右子树没有左子树，那么树的深度应该是其右子树的深度加1。
如果既有右子树又有左子树，那么该树的深度就是气左右子树深度较大值加1。
例如在图1所示的二叉树中，根节点为1的树有左、右两棵子树，其中左、右子树的根节点分别为节点2和节点3。根节点为2的左子树的深度为3，而根节点为3的右子树深度为2，因此，根节点为1的树的深度就是4。这种思路用递归的方法很容易实现。

3. 参考代码 #

#include <iostream>
#include <algorithm>
#include <queue //使用队列
using namespace std;

struct TreeNode {
    int     val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {
    }
};

// 方法一：递归、DFS
class Solution {
public:
    int TreeDepth(TreeNode* pRoot)
    {
        if ( pRoot == nullptr )
            return 0;

        int left = TreeDepth( pRoot->left );
        int right = TreeDepth( pRoot->right );

        return 1 + max( left , right );
    }
};


// 方法二：BFS，层次遍历
class Solution_2 {
public:
    int maxDepth(TreeNode* root) {
        int ans = 0;

        if ( root == nullptr )
            return ans;

        queue<TreeNode*> Q;
        Q.push( root );
        while ( !Q.empty() ) {
            int scale = Q.size();  // 「必须」单独声明
            for ( int i = 0; i < scale; ++i ) {
                TreeNode* cur = Q.front();  Q.pop();
                if ( cur->left )
                    Q.push( cur->left );
                if ( cur->right )
                    Q.push( cur->right );
            }
            ++ans;  // 每一层 +1
        }

        return ans;
    }
};


int main()
{
    TreeNode *head = new TreeNode(5);
    head->left = new TreeNode(3);
    head->right = new TreeNode(8);
    head->left->left = new TreeNode(2);
    head->left->right = new TreeNode(4);
    head->right->left = new TreeNode(7);
    head->right->right = new TreeNode(10);
    head->right->left->left = new TreeNode(6);
    head->right->right->left = new TreeNode(9);
    head->right->right->right = new TreeNode(11);

    Solution solve;

    cout << solve.TreeDepth(head) << endl;

    return 0;
}