主要内容 #

1. 问题描述
2. 求解思路
3. 参考代码

1.问题描述 #

输入两棵二叉树A和B，判断B是不是A的子结构。
例如图1中的两棵二叉树，有一部分子树的结构和B是一样的，因此B是A的子结构。

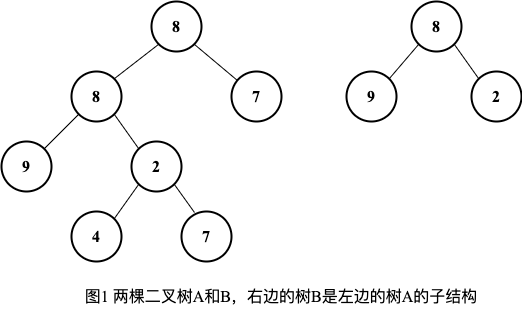
2.求解思路 #

要查找A树中是否存在和B一样的子树，我们可以分两步：

• 在树A中找到和树B的根节点的值一样的节点R；
• 判断树A中以R为根节点的子树是不是包含和树B一样的结构。

以上面图1的两棵树为例来详细分析这个过程。首先试着在树A中找到值为8（树B根节点的值）的节点。从树A得根节点开始遍历，我们发现它的根节点的值就是8。接着判断树A的根节点下面的子树是不是含有和树B一样的结构，如图2所示。在树A中，根节点的左子树的值是8，而树B的根节点的左节点是9，对应的两个节点不同。

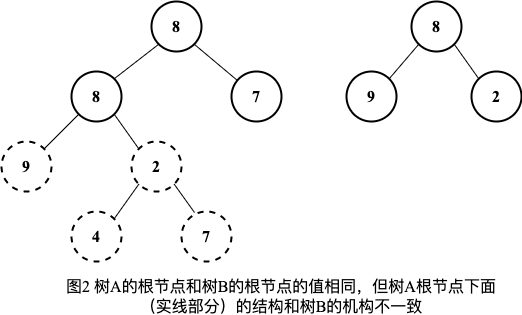
因此我们仍需要遍历树A，接着查找值为8的节点。我们在树的第二层找到了一个值为8的节点，然后进行第二步判断，即判断这个节点下面的子树是否含有和树B一样的结构，如图3所示。于是遍历这个节点下的子树，先后得到两个子节点9和2，这和树B的结构完全相同。此时我们在树A中找到了一棵和树B结构一样的子树，因此树B是树A的子结构。

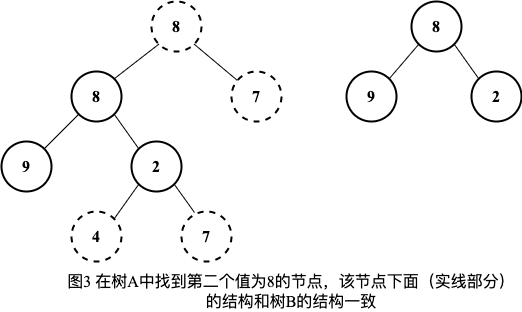
第一步在树A中查找与跟节点的值一样的节点，这实际上就是树的遍历，可以用递归的方法去遍历，也可以用循环的方法去遍历。递归的代码实现比较简洁。

3.参考代码 #

#include <iostream>
#include <queue>
using namespace std;

struct TreeNode {
    double    val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 递归
/* 时间复杂度： O( nm )，空间复杂度：O( m )
*/
class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        bool res = false;

        // 此处相当于「前序」遍历
        if ( A != nullptr && B != nullptr ) {
            if ( A->val == B->val )  // 根节点值相等
                res = DoesTree1HaveTree2( A, B );

            if ( !res )  // 遍历 A 的左子树
                res = isSubStructure( A->left, B );
  
            if ( !res )  // 遍历 A 的右子树
                res = isSubStructure( A->right, B );        
        }

        return res;
    }

    bool DoesTree1HaveTree2( TreeNode* A, TreeNode* B ) {
        if ( B == nullptr )
            return true;
        if ( A == nullptr )  // 此时，B != nullptr 
            return false;
        if ( A->val != B->val )
            return false;
        
        return DoesTree1HaveTree2( A->left, B->left ) && 
               DoesTree1HaveTree2( A->right, B->right );
    }
};