主要内容 #

1. 完全二叉树的定义
2. 完全二叉树的基本性质

1. 完全二叉树的定义 #

如果一颗深度为 k 的二叉树，1 至 k-1 层都是满的，即满足第 i 层（i<k）的节点个数为 2^(i-1)，并且最下面一层的节点都集中在该层最左边的若干位置，则此二叉树称为完全二叉树。
简单的理解
在满二叉树（左图）的最后一层，从右往左擦掉若干（零个）个节点，得到了一棵完全二叉树（右图）。

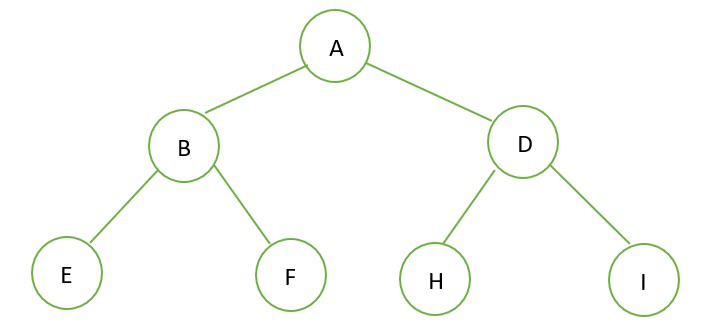满二叉树

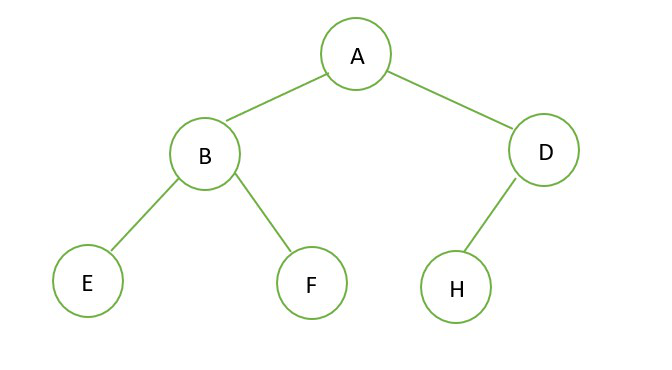完全二叉树

考一考：判断下面三棵树是不是完全二叉树？

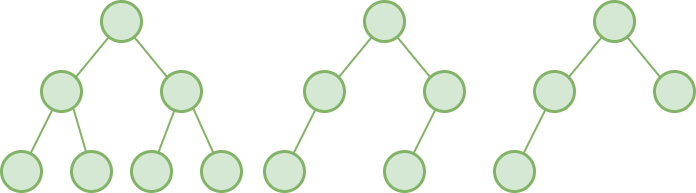
答案：是 否 是

2. 完全二叉树的基本性质 #

性质1：二叉树的第 i 层上至多有 2^(i-1) 个节点，其中 i>=1，比中第三层有 [2^(3-1)] =4 个节点。

性质2：深度为 k 的完全二叉树中至多有 2^(k)-1 个节点。比如深度为 4，有 [2^(4)-1]=7 个节点，此时该二叉树为满二叉树。

性质3：对任意一棵二叉树，如果其叶子结点数，也就是度为 0 的节点数为 n0，度为 2 的结点数为 n2，则n0=n2+1。

性质4：具有 n 个节点的完全二叉树的深度为 floor(log2n)+ 1（其中 floor 表示向下取整）。

性质5：如果对一颗有n个节点的完全二叉树（其深度为 floor(log2n)+ 1）的节点按层序编号，对于任意节点 i 有：

• 如果 i=1，则节点 i 是二叉树的根节点，无双亲；如果 i>1，则其双亲节点是 floor(i/2)；
• 如果 2i>n，则节点 i 无左孩子；否则其左孩子就是 2i；
• 如果 2i+1>n，则节点 i 无有右孩子；否则其右孩子就是 2i+1。