跳至正文
View Categories

< 1 min read

高精度计算算法介绍 #

  1. 高精度计算的概念
  2. 高精度计算的理解
  3. 高精度计算的过程及数据存储方式

收获 #

学完本节内容，可以初步对高精度计算算法的应用场景、概念及计算过程有一个大概的了解。

高精度计算的概念 #

​ 在一般的科学计算中，会经常算到小数点后几百位或者更多，当然也可能是几千亿几百亿的大数字，一般这类数字我们统称为高精度数。高精度算法是用计算机对于超大数据的一种模拟加、减、乘、除、乘方、阶乘、开方等运算。
对于一个很大的数字N >= 10^ 100，很显然这样的数字无法在计算机中正常存储。于是， 我们想到了办法，将这个数字拆开，拆成一位一位的或者是四位四位的存储到一个数组中，用一个数组去表示一个数字。这样这个数字就被称谓是高精度数。 对于高精度数，也要像平常数一样做加减乘除以及乘方的运算，于是就有了高精度算法。
由于计算机输入计算结果的精度通常受到计算机的限制，如：在双精度方式下，计算机最多只能输出16位有效数字，如果超过16位，则只能按浮点形式输出，另外，一般计算机实数表示的范围有限，如果超过这个范围，计算机就无法表示了。但是我们可以通过一些简单的办法来解决这个问题。这就是我们要说的高精度计算。
运行以下代码，并比较结果的差异：

from decimal import Decimal #调用python内置高精度计算包
print((5.55)*100)
print(Decimal(5.55)*100)

高精度计算的理解 #

严格说起来高精度计算并不是一种算法，而是一种思想。这个思想非常朴素，类似于小学知识中的多位数乘法，就是打竖式，如下图所示：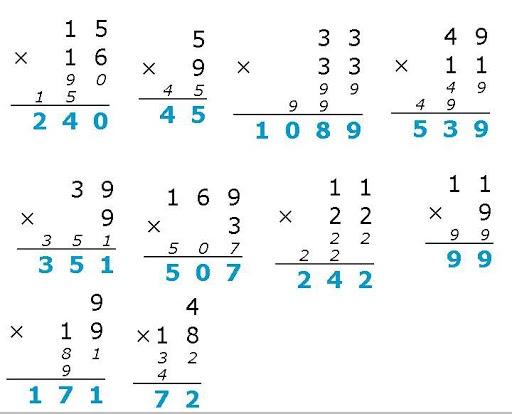

我们人类要打竖式是因为我们只能计算一位数以内的加减乘除，超过一位的人脑不能直接计算，我们就需要用纸笔记录下来进行计算。纸笔计算的方法很简单，就是一位一位地计算，用每一位数字依次去计算乘法，最后再移位相加起来就得到结果了。
比如在上图的第一个例子当中，我们要计算15 * 16，我们先计算6 * 15的结果，再计算1 * 15，最后将两个结果错位相加，就得到了答案。我们要错位的原因也很简单，因为我们在计算15 * 1的时候，其实背后代表的是15 * 10。
我们继续拆分问题，当我们计算6和15相乘的时候，又是怎么计算的呢？顺着这个思路，整个过程可以进一步被划分成先计算6和5相乘，再计算6和1相乘。最后，我们把两个较大数字的相乘拆分成了在每一位上的数字相乘。
到了这里，剩下的就简单了，也就是说我们可以把这两个很大的数字用两个数组来存储，数组当中的每一位存储数字上的一位。比如我们要计算123 * 224， 我们的第一个数组是[1, 2, 3]，我们的第二个数组是[2, 2, 4]。我们仿照乘法竖式中的方法计算这两个数组当中两两的乘积，并将它们错位拼装成答案。
同样,我们用数组来存储中间和最后的结果，最后的结果就是：[2, 7, 5, 5, 2]。这种用数组来模拟数字进行加减乘除运算的方法就叫做高精度算法。

高精度计算的过程及数据存储方式 #

要在计算机上进行高精度计算，首先就应该有精确的输入，即计算机要精确地接收和存储数据。但常用的计算机储存方法无法保存运算超出范围的数字，因此我们联想到了数组的存储使用。
​高精度计算的基本思路如下：
​ 1、以字符串的方式读入数字并保存在字符数组中。
​ 2、计算字符数组中总字符数（高精度数的位数）。
​ 3、将字符串中的字符逐个转化成数字并保存在整型数组a中。运算都会从低位开始 (先算个位，再算十位，依此类推)；在存储时需要倒序存储，也就是个位数存在a[0]，十位数存在a[1]，依此类推。
例如数字4678在数组中存储结构为：
a[0]:8 a[1]:7 a[2]:6 a[3]:4

数据储存的代码实现如下，之后的高精度加减乘除法全部基于此储存方式进行进一步的计算：

#-------------对输入的数字进行数组形式进行倒序储存----------------------
a=input('请输入一个数字a')
b=input('请输入一个数字b')
a1=[0]*10#定义10位的数据长度
b1=[0]*10
la = len(a)
lb= len(b)
#ord()将字符转化为ASCII码；chr()将ASCII码转化为字符
#倒序储存，原因是计算数值从低位算起，即从数组a1[0]处开始计算
for i in range(la):
    a1[i]=ord(a[la-i-1])-ord('0')#将数串a转换为数组a1，并倒序存储(-0对应的相对数值，变成数组储存)
for j in range(lb):
    b1[j] = ord(b[lb-j-1]) - ord('0')

小结 #

理解高精度计算的概念和意义
理解高精度计算的过程，并可以用模拟算数的方法模拟出该过程
理解并实现高精度计算的数据储存过程

习题 #

  1. 习题1：为什么要使用高精度计算算法？
  2. 习题2：请自行比较使用和不使用高精度计算算法下的a=1.8888888;b=2.000001的加法计算结果差别，并进行简单解释
What are your Feelings