主要内容 #
- 中序遍历
- 总结
1. 中序遍历 #
经过上节课的学习我们知道:
二叉排序树也叫二叉搜索树、二叉查找树,简称 BST(Binary Search/Sort Tree)树,它是一种特殊的二叉树,我们重点关注「排序」二字,二叉排序树要求在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值,所以这么看来,二叉排序树是天然有序的。
如果按照中序遍历,得到的结果将是一个从小到大的有序数据集:
void in_order(node root){
node p = root;
if (p != NULL){
in_order(p->left);
printf("%lf\n", p->value);
in_order(p->right);
}
}
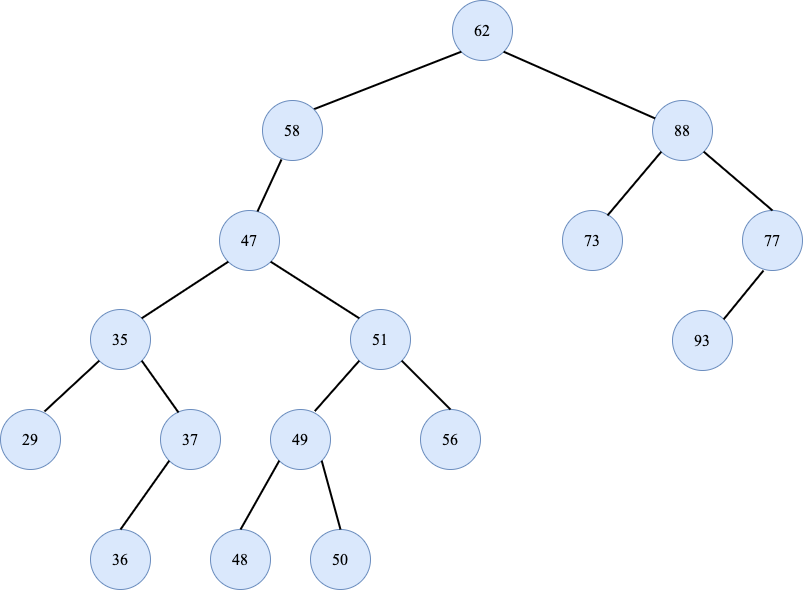
对于上述的序列“62,58,88,47,73,99,35,51,93,29,37,49,56,36,48,50”其中序遍历的结果为:
29.000000 35.000000 36.000000 37.000000 47.000000 48.000000 49.000000 50.000000 51.000000 56.000000 58.000000 63.000000 73.000000 88.000000 93.000000 99.000000
2. 总结 #
二叉排序树是一种实现动态查找表的树形存储结构。同一张查找表中,元素的排序顺序不同,最终构建出的二叉排序树也不一样。
例如,{45,24,53,12,37,93} 和 {12,24,37,45,53,93} 是同一张动态查找表,只是元素的排序顺序不同,它们对应的二叉排序树分别为:
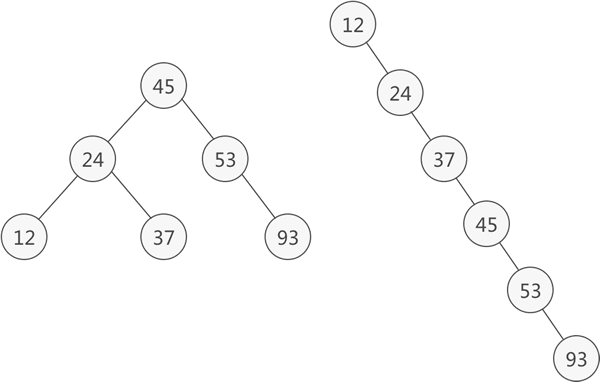
左侧二叉排序树表示的是 {45,24,53,12,37,93},右侧二叉排序树表示的是 {12,24,37,45,53,93}。
这里我们引入平均查找长度的概念:平均查找长度ASL=∑(本层高度*本层元素结点个数)/结点总数
二叉排序树的查找性能和整棵树的形态有关。以上图为例,假设查找表中元素被查找的概率是相等的(都为1/6),左侧二叉排序树的查找性能用平均查找长度(ASL)表示:
ASL = 1/6 * (1+2+2+3+3+3) = 14/6
右侧二叉排序树的查找性能为:
ASL = 1/6 * (1+2+3+4+5+6) = 21/6
ASL 值越小,查找的性能就越高。显然,图 4 左侧二叉排序树的查找性能更高。
也就是说,一张动态查找表往往对应着多棵二叉排序树,当表中元素的查找概率相同时,二叉排序树的层数越少,查找性能越高。



