主要内容 #
- 完全二叉树复习
- 完全二叉树的练习题
1. 完全二叉树复习 #
定义:除了最下层,其他每层都饱满,最下层的结点都集中在该层最左边的若干位置上。
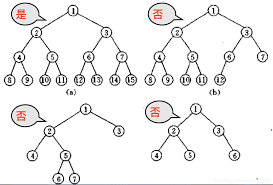
特点:
① 满二叉树是完全二叉树,完全二叉树不一定是满二叉树;
② 在满二叉树的最下层上,从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。
③ 在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。
④若I为结点编号则 如果I>1,则其父结点的编号为I/2;若2*I<=N,则其左儿子(即左子树的根结点)的编号为2*I;若2*I>N,则无左儿子若2*I+1<=N,则其右儿子的结点编号为2*I+1;若2*I+1>N,则无右儿子。
例题1:画一个深度为4的满二叉树。画一个深度为4的完全二叉树。
例题2:具有3个结点的完全二叉树的深度为( 2 )
具有6个结点的完全二叉树的深度为( 3 )
具有8个结点的完全二叉树的深度为( 4 )
具有125个结点的完全二叉树的深度为( 7 )
具有1024个结点的完全二叉树的深度为( 11 )
2. 完全二叉树练习题 #
1.完全二叉树对每个节点从上往下,从左往右编号,第i层的第j个节点的编号是(B)
A 2^i+j B 2^i+j-1 C 2^(i-1)+j D 2^(i-1)+j-1
2.一棵有n个节点的完全二叉树的高度是( )
如果根结点的层次为1 则n个结点二叉树最大高度为n,每层一个结点 最小高度为log2n下取整 + 1
3.二叉树是重要的数据结构,5个点的不同的二叉树有(D)个。
A22 B 30 C 40 D 42
4.完全二叉树的结点个数为4 * N + 3,则它的叶结点个数为(E )。
A 2*N B 2*N-1 C 2*N+1 D 2*N-2 E 2*N+2
节点数是4N+3,所以树枝数是4N+2 因为是完全二叉树,所以不可能有两个节点都含有一个树枝,所以,4N+2个树枝就肯定是来自2N+1个非叶节点;总结点数是4N+3,所以,叶节点有:2N+2个.
5.满二叉树的叶结点个数为N,则它的结点总数为( C)。
A N B 2*N C 2*N–1 D 2*N+1 E 2N–1
6.在有N个叶子节点的哈夫曼树中,其节点总数为(B)
A 不确定 B 2N-1 C 2N+1 D 2N
哈弗曼树也是二叉树,而且树中只有叶子结点跟度为2的结点,由二叉树的性质可得:度为2的结点数量等于叶子结点数量-1,因此结点总数为n+n-1。
7.一棵二叉树高度为h,所有结点的度为0,或为2,则此树最少有( B)个结点
A2^(h-1) B 2^h-1 C 2^h+1 D h+1
节点最少的情况为:除了根节点外,每层都有且仅有2个节点,所以共有2h-1个节点。
8. [多选题]关于二叉树的正确说法是(B C D E)。
A 完全二叉树一定是满二叉树 B 满二叉树一定是完全二叉树
C 深度为h的二叉树最多有2^h-1个结点(h>=1),最少有h个结点
D 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1
E 在二叉树中,第i层的结点总数不超过2^(i-1);
D选项:假设二叉树的0度,1度,2度结点为n0,n1,n2,总节点数为T 则有按照结点求和的 T = n0 + n1 + n2 (1) 按照边求和得: T = n1 + 2 * n2 + 1 (2) 所以 (2) - (1)可得 n2 + 1 - n0 = 0 所以n0 = n2 + 1
9. 完全二叉树的结点个数为11,则它的叶结点个数为(A)
A.4 B.3 C.5 D.2 E. 6
10. 一个高度为h 的二叉树最少结点数目是( E)。
A 2^h+1 B h C 2^h-1 D 2^h E 2^(h-1)



