跳至正文
View Categories

1 min read

高精度计算减法 #

  1. 高精度计算的减法原理
  2. 高精度计算的减法描述
  3. 高精度计算的减法实现

收获 #

学完本节内容，可以初步理解并掌握高精度计算的减法实现。

高精度计算的减法原理 #

在做减法运算时，需要注意的是：被减数必须比减数大，同时需要处理借位。
减法借位原理：当被减数在某位置的数值小于减数数值时，该位置向下一位置借10再相减，下一位置数据-1，原理可以简单表示为：

if a[i]<b[i]) { 
    --a[i+1]; 
    a[i]+=10; 
}
c[i]=a[i]-b[i]；

高精度计算的减法描述 #

写出两个整数相减的竖式表达，如图所示。如果用数组A、B分别存储被减数和减数，用数组C存储结果。
则上例有（A[1]=6，A[2]=5， A[3]=8，B[1]=5，B[2]=5，B[3]=2，C[4]=1，C[3]=1，C[2]=1，C[1]=1）（根据减法具体改）两数相减如图2所示。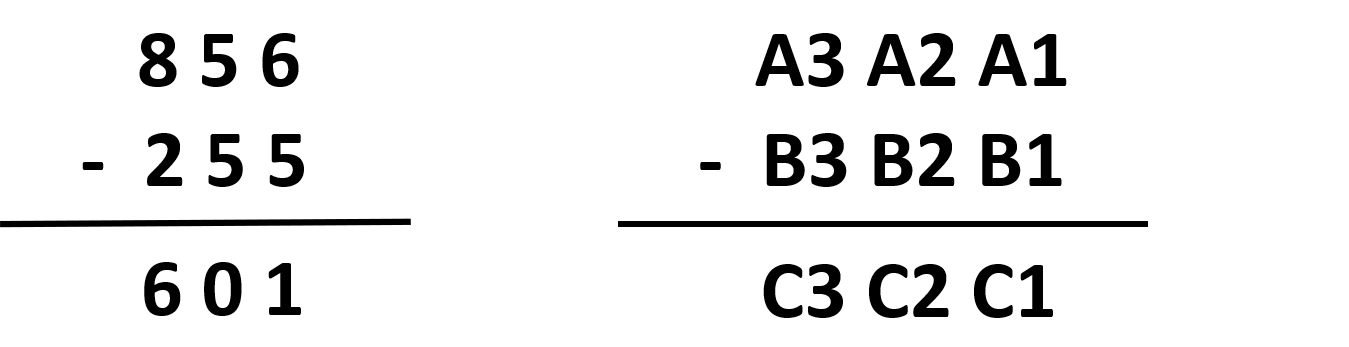

因此，算法描述如下：

int c[10];
void add(int p[],int n[])                  //p,n,c都为数组，分别存储被减数、减数、结果
{
    int  i=1,x=0;                              //x是进位
    while ((i<=p被减数的数组长度))    
　{
　　　　c[i]=p[i]-n[i]+x;       //第i位相减并减上次的借位
     if c[i]<0:              //小于0借位
        x=-1;
　　　　c[i]+=10;                       //存储第i位的值
     else:                   //大于等于0不借位
        x=0;
　　　　i++;                                //位置下标变量
　}
}

高精度计算的减法实现 #

python实现代码如下：

#----------高精度计算之减法运算，注意借位---------
#先确定被减数和减数
num=0#减数初始化
passi_num=0#被减数初始化
la = len(a)#用a[0]计算字符串a的位数
lb= len(b)
if la<lb:#长度更大的位数更多，数值更大
    passi_num=b
    num=a
if la>lb:
    passi_num=a
    num=b
if la==lb:
    passi_num=max(a,b)#max可以直接比较字符串形式的数字大小
    num=min(a,b)
print(passi_num,num)

lp=len(passi_num)#被减数长度
ln=len(num)#减数长度
passi_num1=[0]*10
num1=[0]*10
#ord()将字符转化为ASCII码；chr()将ASCII码转化为字符
#倒序储存，原因是计算数值从低位算起，即从数组a1[0]处开始计算
for i in range(lp):
    passi_num1[i]=ord(passi_num[lp-i-1])-ord('0')#将数串a转换为数组a1，并倒序存储(-0对应的相对数值，变成数组储存)
for j in range(ln):
    num1[j] = ord(num[ln-j-1]) - ord('0')

c=[0]*10#初始化储存数组
clen=0#clen为计算后的位数
x=0#x为借位值
while clen<lp:
    c[clen]=passi_num1[clen]-num1[clen]+x
    if c[clen]<0:#小于0的时候借位
        x=-1#借位
        c[clen] += 10 # 竖式运算，借位补10
    else:
        x=0
    clen+=1
c.reverse()
#删除先导0
while c[0]==0:
      c=c[1:]
print(c)

小结 #

理解并掌握高精度计算减法的原理
用代码实现高精度计算的减法运行

习题 #

  1. 习题1：通过“打竖式”的数学计算方法解释并模拟高精度计算减法
  2. 习题2：仿照高精度计算减法，用代码实现‘1234‘-’876‘的结果
What are your Feelings