主要内容 #
- 基本概念复习
- 完全二叉树的练习题
1. 基本概念复习 #
1. 深度 与 高度 与 度
对于某个结点
- 深度是指结点从根结点到自己的层数(根结点深度为1),
- 高度是指结点所在的最长路径的叶子结点到自己的层数(叶子结点高度为1),
- 度是指结点的儿子分支数。
对于整棵树,最深的叶子结点的深度是树的深度,树根的高度是树的高度,结点中最大的度是树的度。(可见,整棵树的深度和高度是相等的)。
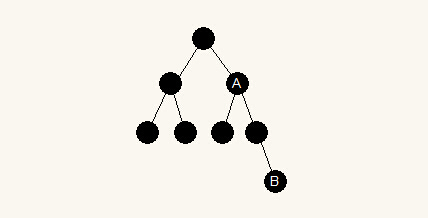
如图:
根结点:深度为1,高度为4,度为2。
A 结点:深度为2,高度为3,度为2。
B 结点:深度为4,高度为1,度为0。
整棵树:深度为4,高度为4,度为2。
总结:
- 空树,深度是1,根结点的度是0度。
- 像上面的满二叉树,深度是2,根结点的度是2度,两个叶结点的度是0度。
- 结点的深度和高度不一定相同,很容易理解,深度是从上而下,高度是自底向上。
- 整棵树而言,深度和高度相等。
2. 完全二叉树的练习题 #
1. 树最适合用来表示()的数据 D
A. 有序 B. 无序 C. 任意元素之间具有多种联系 D. 元素之间具有分支层次关系
2. 树中所有结点的度等于所有结点数加() C
A. 0 B. 1 C. -1 D. 2
3. 假定一颗度为3的树中结点数为50,则其最小高度为() C
A. 3 B. 4 C. 5 D. 6
4. 下列关于二叉树的说法中,正确的是() C
A. 二叉树就是所有结点的度为2的有序树
B. 含有N个结点的二叉树其高度为[log 2 n](向下取整)+1
C. 在完全二叉树中,若一个结点没有左孩子,则它必是叶结点
D. 在任意一颗非空二叉排序树中,删除某结点后又将其插入,则所得二叉排序树与删除前原二叉排序树相同
5. 假设一棵二叉树的结点个数为50,则它的最小高度是() C
A. 4 B. 5 C. 6 D. 7
6. 已知一算术表达式的中缀形式为 A+BC-D/E,后缀形式为 ABC+DE/-,其前缀形式为( ) D
A.-A+BC/DE B. -A+BCD/E C.-+ABC/DE D. -+ABC/DE
7. 设树T的度为4,其中度为1,2,3 和 4 的结点个数分别为 4,2,1,1 则 T 中的叶子数为( ) D
A.5 B.6 C.7 D.8
8. 在下述结论中,正确的是( ) D
①只有一个结点的二叉树的度为 0; ②二叉树的度为 2; ③二叉树的左右子树可任意交换; ④深度为 K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A.①②③ B.②③④ C.②④ D.①④
9. 若一棵二叉树具有 10 个度为 2 的结点,5 个度为 1 的结点,则度为 0 的结点个数是( ) B
A.9 B.11 C.15 D.不确定
10. 具有 10 个叶结点的二叉树中有( )个度为 2 的结点 B
A.8 B.9 C.10 D.ll
11. 有 n 个叶子的哈夫曼树的结点总数为( ) D
A.不确定 B.2n C.2n+1 D.2n-1
12. 设给定权值总数有 n 个,其哈夫曼树的结点总数为( ) D
A.不确定 B.2n C.2n+1 D.2n-1
13. 有关二叉树下列说法正确的是( ) B
A.二叉树的度为 2 B.一棵二叉树的度可以小于 2
C.二叉树中至少有一个结点的度为 2 D.二叉树中任何一个结点的度都为 2
14. 二叉树的第 I 层上最多含有结点数为( ) C
A.2^I B.2^(I-1)-1 C.2^(I-1) D.2^I-1
15. 一个具有 1025 个结点的二叉树的高 h 为( ) C
A.11 B.10 C.11 至 1025 之间 D.10 至 1024 之间
16. 一棵二叉树高度为 h,所有结点的度或为 0,或为 2,则这棵二叉树最少有( )结点 B
A.2h B.2h-1 C.2h+1 D.h+1
17. 一棵具有 n 个结点的完全二叉树的树高度(深度)是( ) A
A.log n+1 B.logn+1 C.logn D.logn-1
18. 深度为 h 的满 m 叉树的第 k 层有( )个结点。 A
A.m^(k-1) B.m^k -1 C.m^(h-1) D.m^h -1
19. 对二叉树的结点从 1 开始进行连续编号,要求每个结点的编号大于其左、右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,可采用( )次序的遍历实现编号。 C
A.先序 B. 中序 C. 后序 D. 从根开始按层次遍历
20. 在下列存储形式中,哪一个不是树的存储形式?( ) D
A.双亲表示法 B.孩子链表表示法 C.孩子兄弟表示法 D.顺序存储表示法
21. 一棵二叉树的前序遍历序列为 ABCDEFG,它的中序遍历序列可能是( ) B
A.CABDEFG B.ABCDEFG C.DACEFBG D.ADCFEG
22. 已知一棵二叉树的前序遍历结果为 ABCDEF,中序遍历结果为 CBAEDF,则后序遍历的结果为( )。 A
A.CBEFDA B. FEDCBA C. CBEDFA D.不定
23. 已知某二叉树的后序遍历序列是 dabec, 中序遍历序列是 debac , 它的前序遍历是( )。 D
A.acbed B.decab C.deabc D.cedba
24. 某二叉树中序序列为 A,B,C,D,E,F,G,后序序列为 B,D,C,A,F,G,E 则前序序列是: B
A.E,G,F,A,C,D,B B.E,A,C,B,D,G,F C.E,A,G,C,F,B,D D.上面的都不对
25. 二叉树的先序遍历和中序遍历如下: 先序遍历:EFHIGJK;中序遍历: HFIEJKG 。该二叉树根的右子树的根是: C
A、 E B、 F C、 G D、 H
26. 引入二叉线索树的目的是( ) A
A.加快查找结点的前驱或后继的速度 B.为了能在二叉树中方便的进行插入与删除
C.为了能方便的找到双亲 D.使二叉树的遍历结果唯一
27. 线索二叉树是一种( )结构 C
A. 逻辑 B. 逻辑和存储 C. 物理 D.线性
28. 由 3 个结点可以构造出多少种不同的二叉树?( ) D
A.2 B.3 C.4 D.5
29. 下述编码中哪一个不是前缀码( ) B
A.(00,01,10,11) B.(0,1,00,11)
C.(0,10,110,111) D.(1,01,000,001)



