堆排序算法基础 #
- 堆排序算法介绍
- 树的原理
- 二叉树介绍
收获 #
学完本节内容,可以初步理解并掌握堆排序算法。
堆排序算法介绍 #
堆排序(Heap Sort)是利用堆这种数据结构所设计的一种排序算法。
堆的结构是一棵完全二叉树的结构,并且满足堆积的性质:每个节点(叶节点除外)的值都大于等于(或都小于等于)它的子节点。
堆排序先按从上到下、从左到右的顺序将待排序列表中的元素构造成一棵完全二叉树,然后对完全二叉树进行调整,使其满足堆积的性质:每个节点(叶节点除外)的值都大于等于(或都小于等于)它的子节点。构建出堆后,将堆顶与堆尾进行交换,然后将堆尾从堆中取出来,取出来的数据就是最大(或最小)的数据。重复构建堆并将堆顶和堆尾进行交换,取出堆尾的数据,直到堆中的数据全部被取出,列表排序完成。
树的原理 #
一个标准的树的结构如下图所示: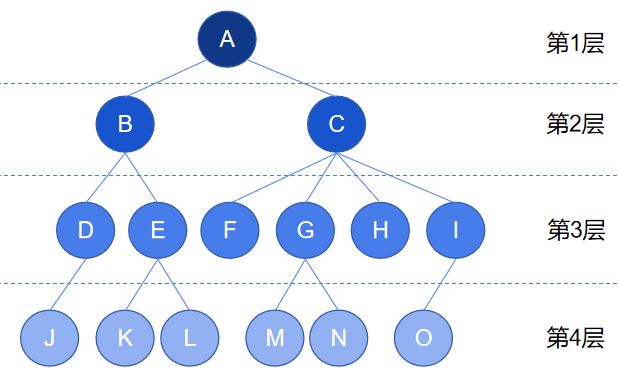
树(Tree)是一种抽象的数据结构,是一个数据的集合,集合中的数据组成了一个树状结构。例如上图,看起来像一棵倒挂的树,根朝上叶朝下。
树是由n(n>=0)个节点组成的具有层次关系的数据集合。当 n=0 时,树中没有节点,称为空树。当 n>0 时,有且仅有一个节点被称为根节点(Root),如果 n=1 ,树只有根节点一个节点。如果 n>1 ,除根节点外,将其余的节点分成m(m>0)个互不相交的数据集合,这 m 个集合每一个都要满足树的结构(有且仅有一个根节点),并且这 m 棵树都“挂”在根节点上,如此递归下去,直到所有节点都“挂”到这棵树上。其中,这 m 个集合构成的 m 棵树都被称为根节点的子树。
在理解树的结构和定义时,需要运用到递归的思想。以上图为例,树的节点集合为 {A,B,C,D,E,F,G,H…} ,n=15,根节点为 A ,除根节点 A 外,其余节点组成了两个(m=2)集合(m1和m2),
m1集合为 {B,D,E,J,K,L} ,m2集合为 {C,F,G,H,I,M,N,O} 。在m1中,B 为m1的根节点,除 B 以外,其余节点组成两个集合m3,m4,集合m3={D,E,J,K,L} 和集合m4={F,G,H,I,M,N,O} ,以此类推….
在这个过程中,生成的子集合m1,m2为A的子树,B,C为A的子节点。
一些重要的概念定义如下:
节点的度:一个节点含有的子树(或子节点)的个数称为该节点的度。例如上图中, 根节点 A 的度为2,节点 C 的度为4,节点I的度为1,节点O的度为0。
叶节点:又称为终端节点,度为0的节点被称为叶节点。例如上图中,第四层的节点都是叶节点。
二叉树介绍 #
二叉树是每个节点最多有两个子树的树结构,是一种特殊的树。只要树中所有节点的子树都不超过两个(0个,1个,2个),这就是一棵普通的二叉树。
在二叉树中,有一些比较特殊,除了满足二叉树的结构外,还满足一些特殊的规则。例如,完全二叉树,设其树的深度为d(d>1),除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树。
一种典型的二叉树如下图所示。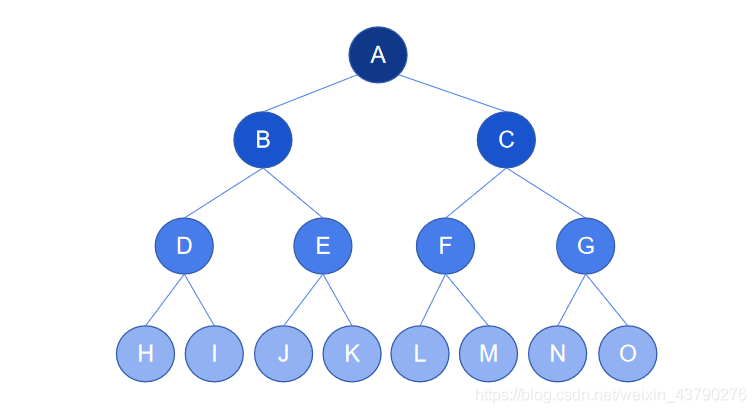
小结 #
理解树及二叉树的基本概念
理解堆排序的基本概念
习题 #
- 习题1:画出一个典型的二叉树
- 习题2:描述堆排序算法的概念



