计数排序算法 #

1. 计数排序算法介绍
2. 计数排序算法原理
3. 计数排序算法的实现

收获 #

学完本节内容，可以初步理解并掌握计数排序算法。

计数排序算法介绍 #

计数排序(Counting Sort)是一种不比较数据大小的排序算法，是一种牺牲空间换取时间的排序算法。

计数排序适合数据量大且数据范围小的数据排序，如对人的年龄进行排序，对考试成绩进行排序等。

计数排序先找到待排序列表中的最大值 k，开辟一个长度为 k+1 的计数列表，计数列表中的所有初始值都为 0。走访待排序列表，如果走访到的元素值为 i，则计数列表中索引 i 的值加1，走访完整个待排序列表，就可以统计出待排序列表中每个值的数量。然后创建一个新列表，根据计数列表中统计的数量，依次在新列表中添加对应数量的 i ，得到排好序的列表。

计数排序算法原理 #

计数排序的原理如下：

1. 找到待排序列表中的最大值 k，开辟一个长度为 k+1 的计数列表，计数列表中的值都为 0。初始列表及相应的计数空间如下图所示
   
   
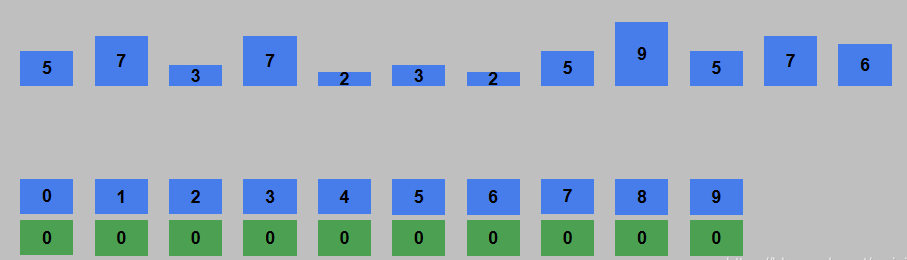
2. 走访待排序列表，如果走访到的元素值为 i，则计数列表中索引 i 的值加1。
3. 走访完整个待排序列表，计数列表中索引 i 的值 j 表示 i 的个数为 j，统计出待排序列表中每个值的数量。如下图所示
   
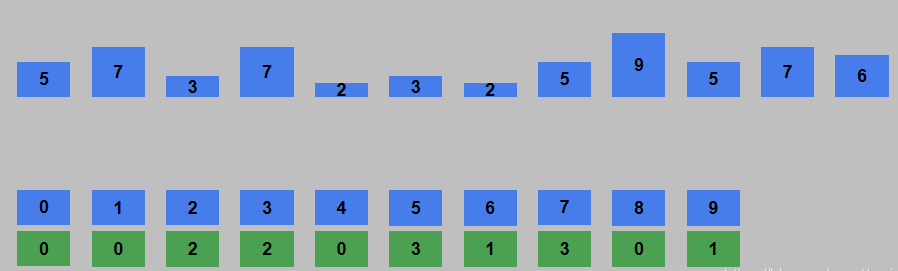
4. 创建一个新列表，遍历计数列表，依次在新列表中添加 j 个 i，新列表就是排好序后的列表，整个过程没有比较待排序列表中的数据大小。如下图所示
   

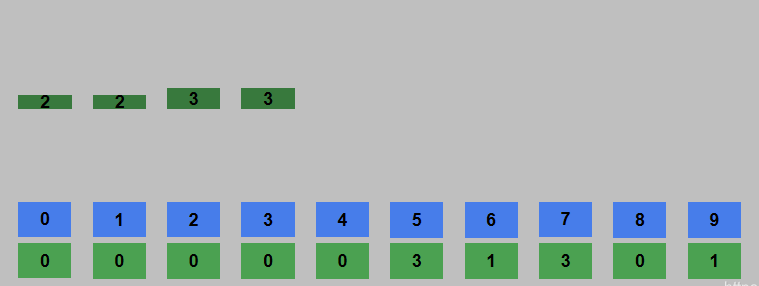
计数排序算法的实现 #

python实现代码如下：

def counting_sort(a):
    if len(a) < 2:
        return a
    max_num = max(a)
    count = [0] * (max_num + 1) 
    for num in a:
        count[num] += 1 #计数
    new_a = list()
    for i in range(len(count)):
        for j in range(count[i]):
            new_a.append(i)
    return new_a


if __name__ == '__main__':
    a = [5, 7, 3, 7, 2, 3, 2, 5, 9, 5, 7, 6]
    print(counting_sort(a))

小结 #

理解并掌握计数排序算法的原理
掌握计数排序的代码实现

习题 #

1. 习题1：画出计数排序算法的流程图
2. 习题2：使用计数排序算法，对列表[10, 17, 50, 7, 7, 24, 27, 10, 15, 5, 36,5]进行升序排列