排序算法总结1 #
- python内置函数排序实现
- 排序算法的分类
- 排序算法的稳定性
收获 #
学完本节内容,可以对排序算法有更全面的了解。
python内置函数排序实现 #
python中,有一个自带的内置函数,可以实现排序,其调用形式为:
list=[1,5,3,2] list.sort() print(list) 或者 list_new=sorted(list) print(list_new)
其实现的内部机制为Timesort,其最坏时间复杂度为O(n log n),空间复杂度为O(n)
排序算法的分类 #
排序算法大致可分为两类,非线性时间比较类排序和线性时间非比较类排序。其中,非线性时间比较类排序又可以分为交换类,插入类,选择类排序和归并排序。如下图所示。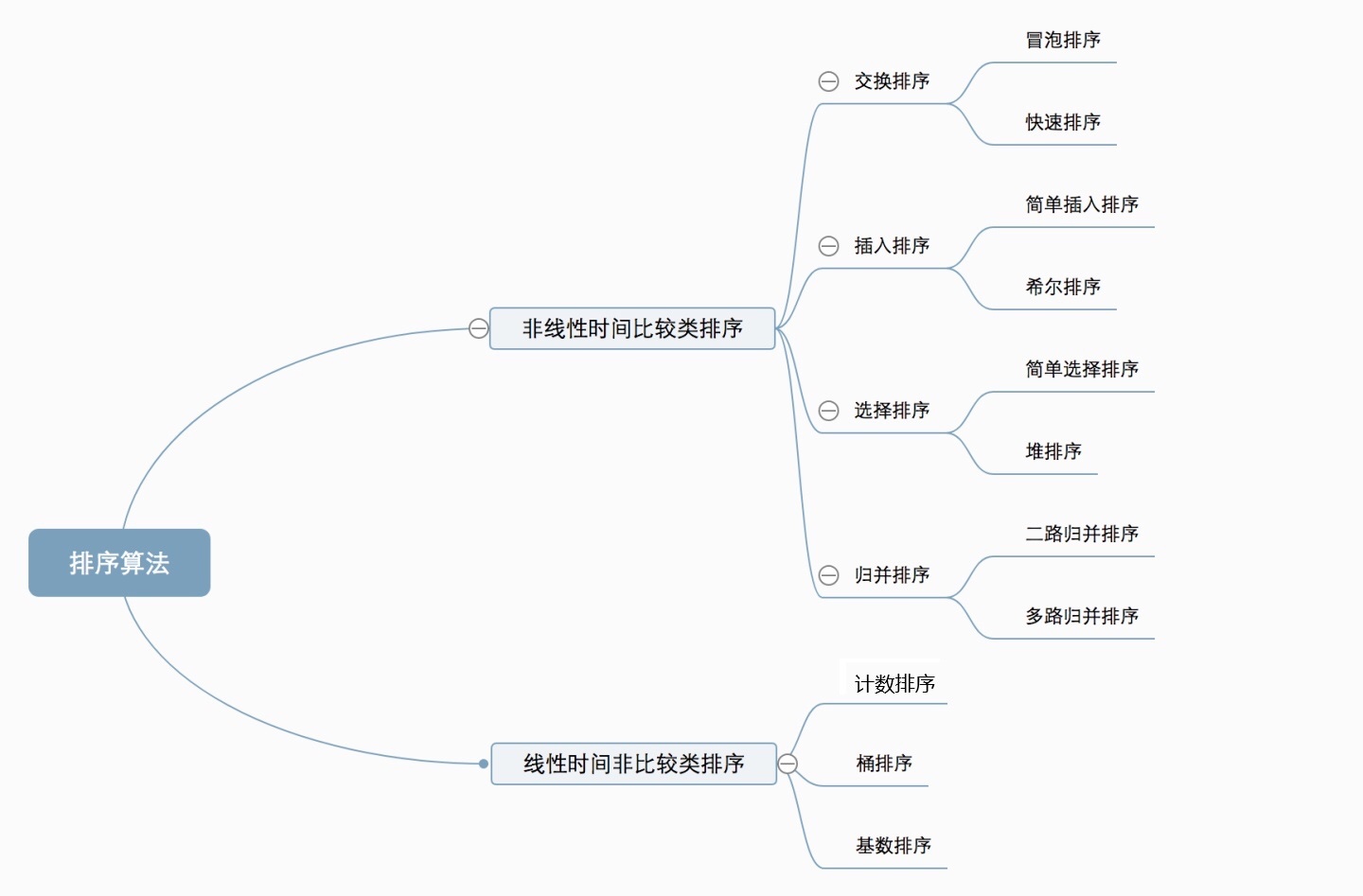
排序算法的稳定性 #
排序算法的稳定性指,当元素列表中有相等的元素时,相等元素的相对次序是否固定不变,如果相对次序固定不变,则排序算法是稳定的,反之亦然。
常见的几种排序算法的稳定性表现如下:
冒泡排序:在冒泡排序中,每次比较两个元素,当元素的大小顺序错误时才会进行交换,如果元素列表中有两个相等的元素,它们最终肯定会相邻在一起,但对它们比较时不会进行交换,相对次序是保持不变的。所以冒泡排序是一种稳定的排序算法。
快速排序:在快速排序的实现过程中,有两个游标从列表的两边向中间移动,游标right向左移动的过程中,如果数据小于基准数据,则会将数据赋值给left游标。在这个过程中,如果有相等的数据,相对位置很可能会发生变化,如 [10, 5, 5] 。所以快速排序是一种不稳定的排序算法。
插入排序:在插入排序中,每次将一个未排序的数据插入到已排序序列中,插入的方式是从后到前依次比较和交换,如果元素列表中有两个相等的元素,不会进行交换,相对次序是保持不变的。所以插入排序是一种稳定的排序算法。
希尔排序:在希尔排序中,会进行多次分组插入排序,每一次组内的插入排序是稳定的,不会改变元素的相对次序。但在多次的分组排序中,相同的元素在各自的组内插入排序中移动,相对次序很可能会被打乱。所以希尔排序是一种不稳定的排序算法。
选择排序:在选择排序中,每次都是选择未排序序列中的最小元素,交换到未排序序列的起始位置。存在相等的元素时,如果最小的元素都比它们靠后,最小的元素与相对位置靠前的元素进行交换,则它们的相对位置就发生了变化。如 [10, 10, 5],进行选择排序后两个 10 的相对位置发生了变化。所以选择排序是一种不稳定的排序算法。
堆排序:在堆排序中,会交换节点与子节点,如果有相等的数据,可能会改变相等数据的相对次序。所以堆排序是一种不稳定的排序算法。
归并排序:在归并排序合并的过程中,如果有相等的数据,会先添加左表的数据到新列表中,再添加右表的数据,这不会改变相等数据的相对位置。所以归并排序是一种稳定的排序算法。
桶排序:根据桶排序的排序原理,会将待排序列表进行分桶、桶内排序和合并。在对每一个桶进行桶内排序时,可以采用不同的排序算法,有些排序算法是稳定的,有些排序算法是不稳定,这会影响到桶排序的稳定性。所以桶排序的稳定性取决于桶内排序算法的稳定性。
计数排序:根据计数排序的应用场景,待排序列表中有很多值相等的元素。不过,计数排序没有比较待排序列表中的数据大小,也没有进行位置交换,相等数据的相对次序是保持不变的。所以计数排序是一种稳定的排序算法。
可以通过以下程序对三种常见的排序算法(冒泡排序,快速排序,插入排序)的稳定性进行实验探索:
import numpy as np
import time
import random
def bubblesort(a): #冒泡排序
n=len(a)
ind=[k for k in range(len(a))]#建立一个索引矩阵
for i in range(n):
for j in range(0,n-i-1):
if a[j]>a[j+1]:
a[j],a[j+1]=a[j+1],a[j]#交换位置
ind[j],ind[j+1]=ind[j+1],ind[j]#交换位置
return a,ind
def quicksortind(a,ind,start,end):
#ind = [k for k in range(len(a))] #建立一个索引矩阵
if start>=end:#当子序列包含一个或0个点的时候,停止排序,认为排序完成
return
base=a[start]#选取一个种子点,一般从最左边开始
#left=0#初始的左index
#right=n-1#初始的右index
left,right=start,end
while left<right:#第一次能否进入循环的判断
while a[right]>=base and left<right:#进入循环后,right值在不断变化,需要重新添加跳出循环的条件(and left<right)
right-=1
a[left]=a[right]#当右指针检索到小于base的数值时,暂停检索,并将其数值赋值给左指针位置的数值
ind[left],ind[right]=ind[right],ind[left]#交换索引
while a[left]<=base and left<right:
left+=1
a[right]=a[left]#当左指针检索到大于base的数值时,暂停检索,并将其数值赋值给右指针位置的数值
ind[right],ind[left]=ind[left],ind[right]#交换索引
a[left]=base#当left=right时,把base插入left位置,完成第一轮排序
ind[left],ind[start]=ind[start],ind[left]
#以下用递归思想依次对子序列进行快速排序(重复上述操作)
quicksortind(a,ind,start,left-1)
quicksortind(a,ind,left+1,end)
def insertsort(a):# 插入排序
l = len(a)
min_index = 0
ind = [k for k in range(len(a))]
for i in range(1, l):
value = a[i] # 保存新的未排序的点的值
j = i - 1 # 已排序的最后一个数(前一个)
#min_value = a[i]
while j >= 0 and a[j+1] < a[j]:
a[j + 1], a[j] = a[j], a[j + 1]
ind[j + 1], ind[j] = ind[j], ind[j + 1]
j -= 1
return a,ind
'''
稳定性比较
'''
if __name__=='__main__':
a = [5, 5, 5, 4, 2, 3, 2, 4, 3]
a1,ind1=bubblesort(a)
print(a1)
print(ind1)
a = [5, 5, 5, 4, 2, 3, 2, 4, 3]
ind = [k for k in range(len(a))] # 建立一个索引矩阵
quicksortind(a,ind, 0, len(a) - 1)
print(a)
print(ind)
a=[5,5,5,4,2,3,2,4,3]
a3,ind3=insertsort(a)
print(a3)
print(ind3)
小结 #
掌握python内置函数sort(),sorted()的用法
巩固并加深对不同排序算法的理解
习题 #
- 习题1:使用pyton内置函数对列表list=[10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]进行排序
- 习题2:简述排序算法的分类,及几种常见排序算法所属的类别



