排序算法总结2 #
- 排序算法的时间复杂度
- 排序算法的空间复杂度
- 排序算法的性能总结
收获 #
学完本节内容,可以对排序算法有更全面的了解。
排序算法的时间复杂度 #
时间复杂度描述了算法的运行时间,考察的是当输入值大小趋近无穷时的情况。在没有特殊说明时,一般都是计算最坏时间复杂度。计算时间复杂度的过程,常常需要分析一个算法运行过程中需要的基本操作,计量所有操作的数量。
冒泡排序:在冒泡排序中,最坏的情况是元素列表的初始状态是完全逆序排列的,需要进行 n-1 轮“冒泡”,每一轮“冒泡”需要进行 n-i 次比较和交换操作。i 的平均值为 n/2 ,时间复杂度为 T(n)=n(n-1)/2 ,再乘每次操作的步骤数(常数,不影响大O记法),所以冒泡排序的时间复杂度为 O(n^2) 。
快速排序:在快速排序中,最坏的情况是元素列表的初始状态是完全逆序排列的,这使得每次分割所得的子表中一个为空表,另一个的长度为原表的长度减1,所以需要进行 n 轮分割,每一轮需要进行 n/2 次比较。时间复杂度为 T(n)=n(n-1)/2 ,再乘每次操作的步骤数(常数,不影响大O记法),所以快速排序的时间复杂度为 O(n^2) 。
插入排序:在插入排序中,最坏的情况是元素列表的初始状态是完全逆序排列的,每一轮插入都需要移动到最左端,需要进行 n-1 轮“插入”,每一轮“插入”需要向前比较和移动 i 次,i 的平均值为 n/2 ,时间复杂度为 T(n)=n(n-1)/2 ,再乘每次操作的步骤数(常数,不影响大O记法),所以插入排序的时间复杂度为 O(n^2) 。
希尔排序:希尔排序的时间复杂度没有插入排序那么直观,因为在希尔排序中,对数据进行分组排序的增量序列是不确定的。这里我们参考前人总结的经验,希尔排序的时间复杂度为 O(n^1.5) 。
选择排序:在选择排序中,不管待排序列表的初始状态如何,都不影响排序的时间复杂度。选择排序需要进行 n-1 轮排序,每一轮排序需要进行 n-i 次比较,i 的平均值是 n/2 ,时间复杂度为 T(n)=n(n-1)/2 ,再乘每次操作的步骤数(常数,不影响大O记法),所以选择排序的时间复杂度为 O(n^2) 。
堆排序:在堆排序中,构建一次大顶堆可以取出一个元素,完成一轮堆排序,一共需要进行n轮堆排序。每次构建大顶堆时,需要进行的比较和交换次数平均为logn(第一轮构建堆时步骤多,后面重建堆时步骤会少很多)。时间复杂度为 T(n)=nlogn ,再乘每次操作的步骤数(常数,不影响大O记法),所以堆排序的时间复杂度为 O(nlogn) 。
归并排序:在归并排序中,不管待排序列表的初始状态如何,都不影响排序的时间复杂度。归并排序一直对待排序列表进行拆分,需要进行logn次拆分,在每一次递归合并中,需要进行n次比较和添加。时间复杂度为 T(n)=nlogn ,再乘每次操作的步骤数(常数,不影响大O记法),所以归并排序的时间复杂度为 O(nlogn) 。
桶排序:在桶排序中,需要走访待排序列表中的每一个元素,进行分桶,列表长度为 n ,然后需要对每一个桶进行桶内排序,单个桶内排序的最坏时间复杂度是 O(ni^2),ni 表示第 i 个桶内有 ni 个数据,一共有 k 个桶,时间复杂度为n加每一个桶内排序的时间复杂度,最坏情况下所有数据全被分到了一个桶内,ni=n,时间复杂度为T(n)=n+n^2,再乘分桶和排序的步骤数(常数,不影响大O记法),所以桶排序的时间复杂度为 O(n^2) 。
计数排序:在计数排序中,需要走访待排序列表中的每一个元素,进行计数,列表长度为 n ,然后需要遍历计数列表,添加数据到新列表中,计数列表长度为 k+1 ,时间复杂度为 T(n)=n+k+1,再乘计数和添加数据的步骤数(常数,不影响大O记法),所以计数排序的时间复杂度为 O(n+k) 。
可以通过以下程序对三种常见的排序算法(冒泡排序,快速排序,插入排序)的时间复杂度进行实验探索:
import numpy as np
import time
import random
import copy
def bubblesort(a): #冒泡排序
n=len(a)
for i in range(n):
for j in range(0,n-i-1):
if a[j]>=a[j+1]:
a[j],a[j+1]=a[j+1],a[j]
return a
def quicksort(a,start,end):
if start>=end:#当子序列包含一个或0个点的时候,停止排序,认为排序完成
return
base=a[start]#选取一个种子点,一般从最左边开始
left,right=start,end
while left<right:#第一次能否进入循环的判断
while a[right]>=base and left<right:#进入循环后,right值在不断变化,需要重新添加跳出循环的条件(and left<right)
right-=1
a[left]=a[right]#当右指针检索到小于base的数值时,暂停检索,并将其数值赋值给左指针位置的数值
while a[left]<=base and left<right:
left+=1
a[right]=a[left]#当左指针检索到大于base的数值时,暂停检索,并将其数值赋值给右指针位置的数值
a[left]=base#当left=right时,把base插入left位置,完成第一轮排序
#以下用递归思想依次对子序列进行快速排序 (重复上述操作)
quicksort(a,start,left-1)
quicksort(a,left+1,end)
def insertsort(a):# 插入排序
n = len(a)
min_index = 0
for i in range(1, n):
value = a[i] # 保存新的未排序的点的值
j = i - 1 # 已排序的最后一个数(前一个)
while j >= 0 and value < a[j]:
min_index = j # 当未排序的值<前一个值时,保留前一个值的index信息为局部最小位置
a[min_index + 1] = a[j] # 该最小位置的后一个值为原来在该位置上的排序好的值(这样就实现了“插入”)
j -= 1 # 再在已排序好的数字中继续向前检索
a[min_index] = value
return a
'''
时间复杂度比较
这里有个很有趣的现象,当数据量比较小的时候,插入排序的速度>快速排序
'''
if __name__=='__main__':
#随机生成10000个数字
a=list(np.random.randint(1,10000,10000))
# a1=[]
# for i in range(10000):
# a1.append(random.randint(1,100000))
#拷贝,创造两个独立的对象
#a2=copy.copy(a1)#浅拷贝
a1=copy.deepcopy(a)
a2=copy.deepcopy(a)
a3=copy.deepcopy(a)
#计时开始
start1=time.time()
print('排序前的a1:', a1)
bubblesort(a1)
print('排序后的a1:', a1)
#计时结束
end1=time.time()
print('冒泡排序所用的总时长',end1-start1,'s')
#计时开始
start2=time.time()
print('排序前的a2:',a2)
quicksort(a2, 0, len(a2) - 1)
print('排序后的a3:',a2)
#计时结束
end2=time.time()
print('快速排序所用的总时长',end2-start2,'s')
#计时开始
start3=time.time()
print('排序前的a3:',a3)
insertsort(a3)
print('排序后的a3:',a3)
#计时结束
end3=time.time()
print('插入排序所用的总时长',end3-start3,'s')
排序算法的空间复杂度 #
类似于时间复杂度的计算,空间复杂度主要通过开辟新的空间来换取时间。
相比于时间复杂度,空间复杂度的计算相对比较简单,主要通过计算其所占用的空间来进行评估。
空间复杂度是指算法在计算机内执行时所需存储空间的度量,它也是问题规模n的函数
空间复杂度O(1):当一个算法的空间复杂度为一个常量,即不随被处理数据量n的大小而改变时,可表示为O(1)。典型的此类排序算法包括交换类排序的冒泡排序算法,插入类排序的两种算法,选择类排序的两种算法。
空间复杂度O(log n):当一个算法的空间复杂度与以2为底的n的对数成正比时,可表示为O(log n)。典型的此类排序算法有快速排序算法。
空间复杂度O(n):当一个算法的空间复杂度与n成线性比例关系时,可表示为O(n)。典型的此类排序算法包括归并排序和桶排序。 排序算法的性能总结
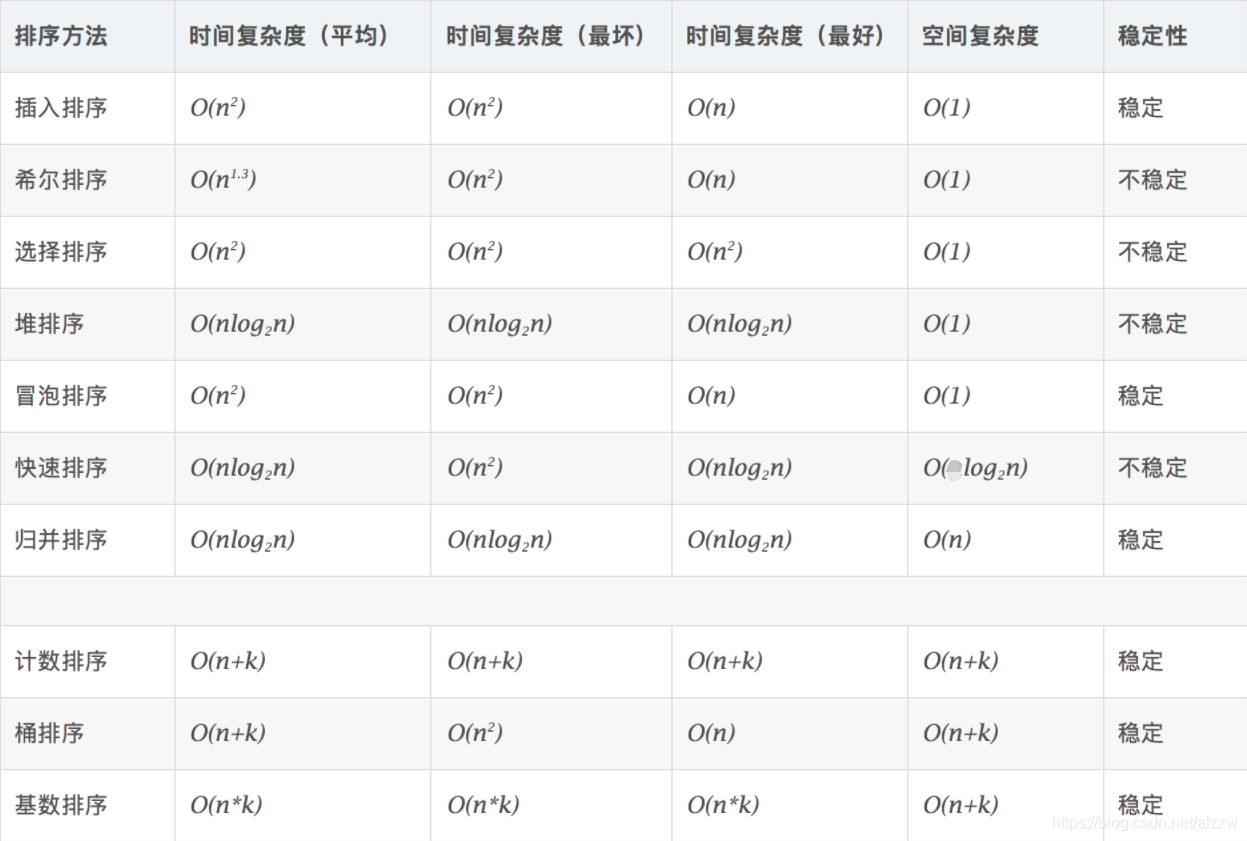
几种常见的排序算法的稳定性、时间及空间复杂度评估如下图所示:
小结 #
进一步理解排序算法的复杂度评估
了解几种常见排序算法的性能表现,并可以根据需求选择合适的排序算法
习题 #
- 习题1:列出空间复杂度为O(1)的几种排序算法
- 习题2:列出时间复杂度最低的几种排序算法



