汉诺塔问题 #

1. 汉诺塔问题介绍
2. 汉诺塔问题分析
3. 汉诺塔问题的实现

收获 #

学完本节内容，可以初步理解并掌握汉诺塔问题的原理及实现。

汉诺塔问题介绍 #

汉诺塔源于古老的印度传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
该问题可以简化为：假设有A,B,C三根柱子，如何移动可以将全部的A移动到C上？

汉诺塔问题分析 #

可以采用逆推方式进行分析，其步骤如下：
（1）将n个圆盘分解为两部分，第n个圆盘和前（n-1）个圆盘，第一次移动将前（n-1）个圆盘经过C移动到B上。这里记为移动过程。如下图所示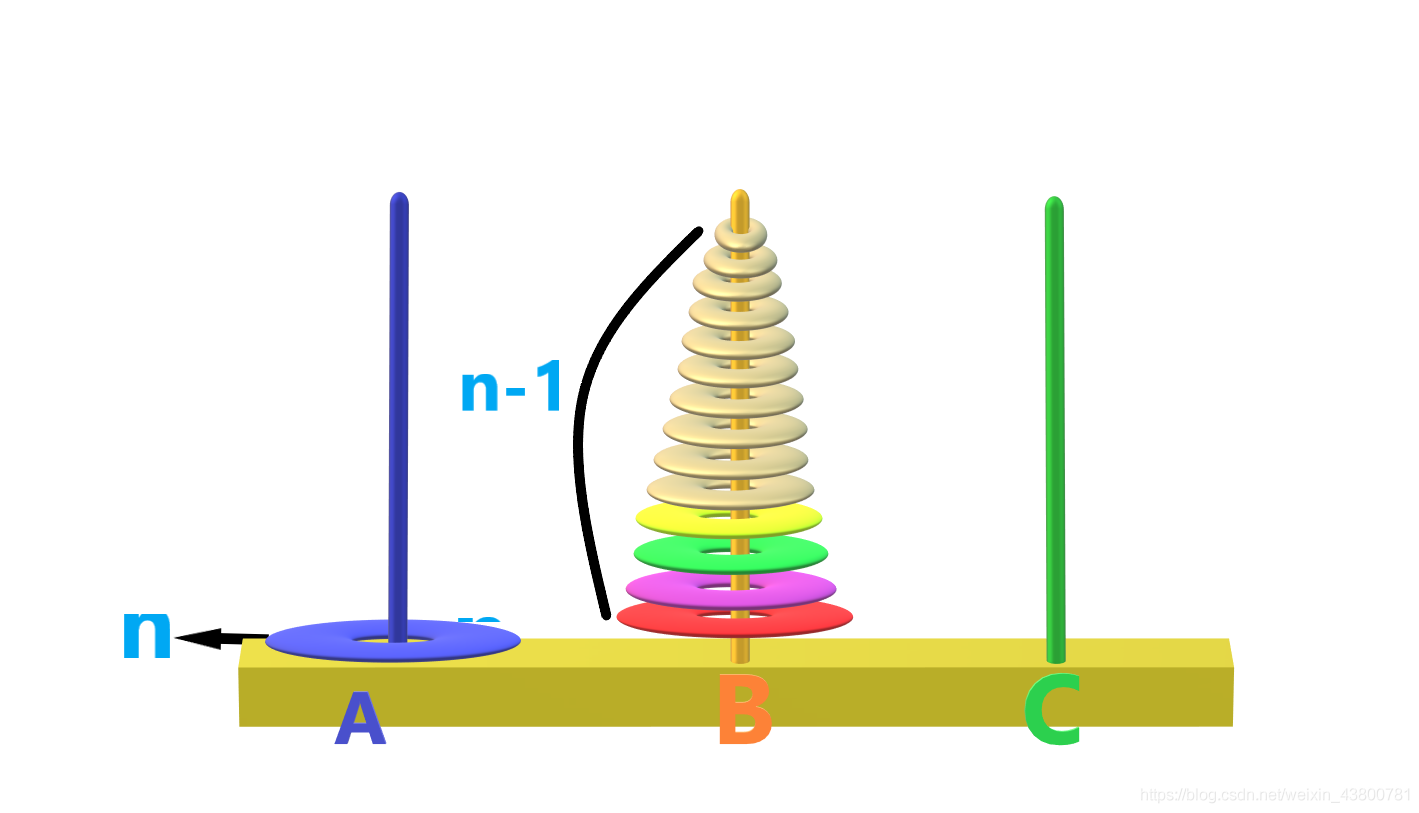

（2）将第n个圆盘移动到目标C上。如下图所示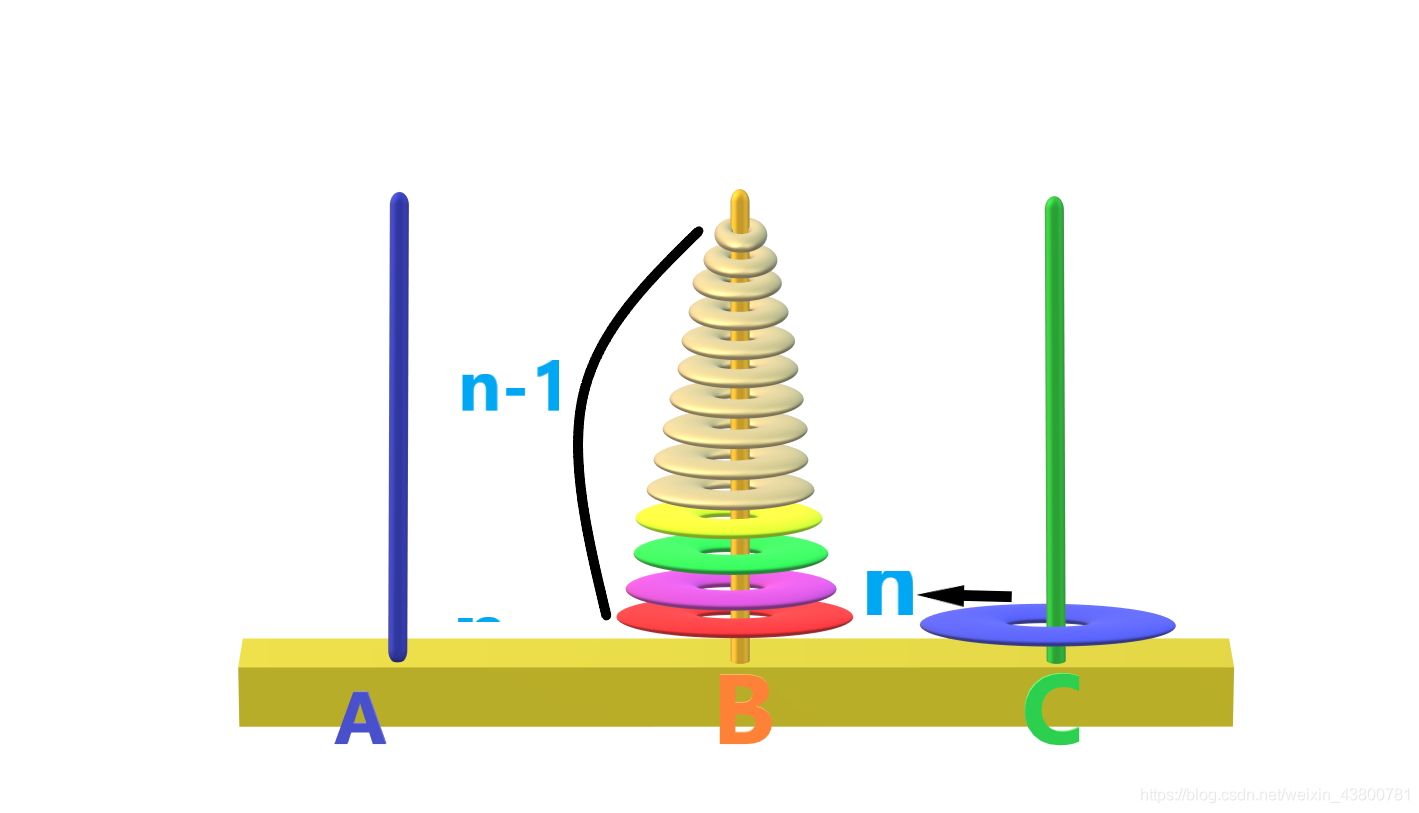

（3）将在B上的前（n-1）个圆盘经过A移动到目标C上。如下图所示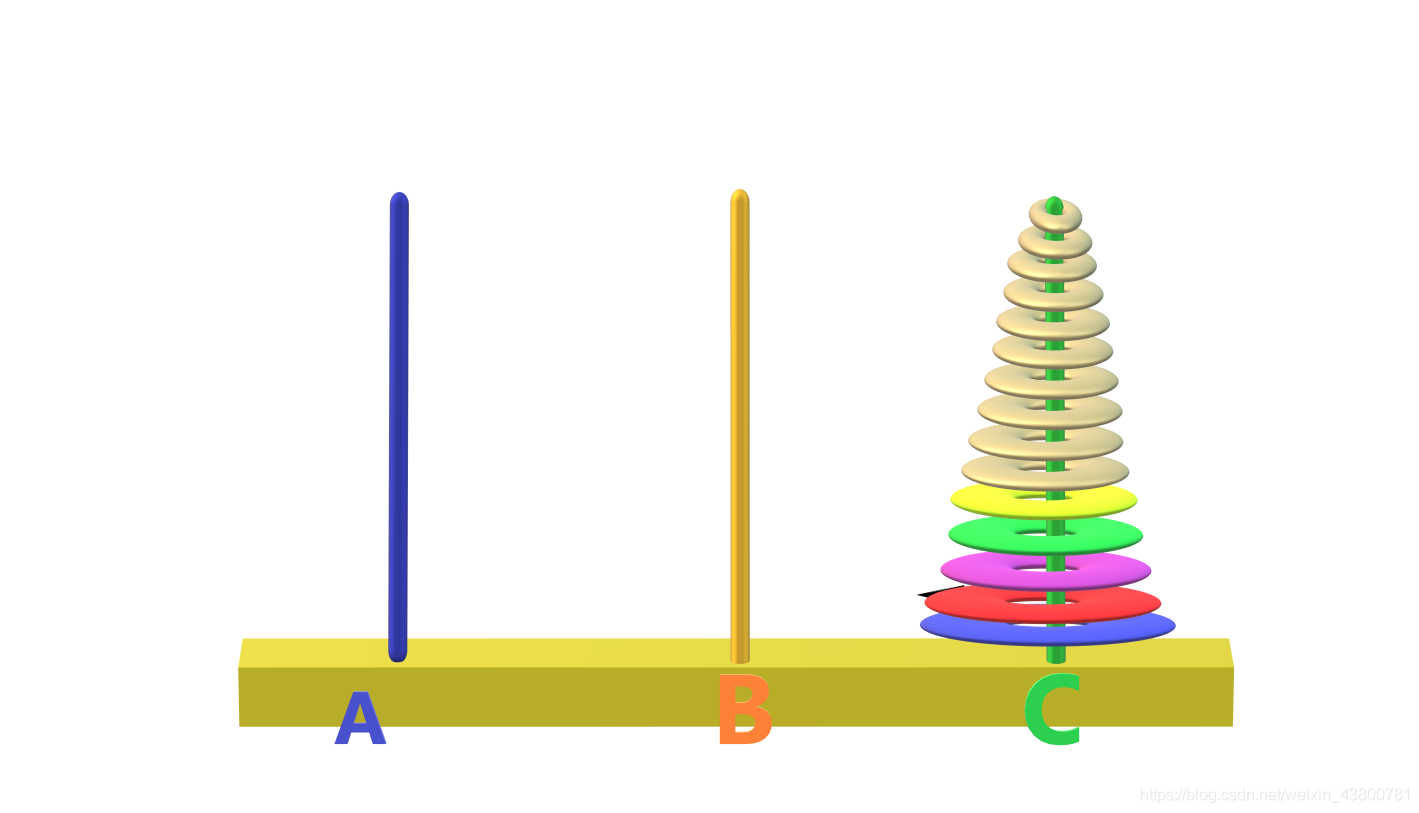

（4）重复步骤（1）、（2）、（3），直到完成最后一个圆盘的移动

汉诺塔问题的实现 #

python实现代码如下：

def hanoi(n,start,transfer,end):
    if n==1:
        print(start,'->',end)
        return
    if n==2:
        print(start,'->',transfer)
        print(start,'->',end)
        print(transfer,'->',end)
        return
    #n>=3时，从start到end的转移需要以下3步：
    #把前n-1个盘子（从start开始）经过end，移动到transfer上（这时end被当作了暂时的中转站）
    hanoi(n-1,start,end,transfer)
    #把第n个盘子移动到end上(每次移动的最大的底部，之后不变化)
    print(start,'->',end)
    #把前n-1个盘子(从transfer开始)经过start，移动到end上
    hanoi(n-1,transfer,start,end)

if __name__=='__main__':
    hanoi(3,'A','B','C')

小结 #

理解并掌握汉诺塔问题的思想
掌握汉诺塔问题的代码实现

习题 #

1. 习题1：画出汉诺塔问题的流程图
2. 习题2：求解移动n个盘子的汉诺塔问题共需要多少次操作？