平面分隔问题1——直线分隔 #

1. 直线分隔问题介绍
2. 直线分隔问题分析
3. 直线分隔问题的实现

收获 #

学完本节内容，可以初步理解并掌握直线分隔问题的原理及实现。

直线分隔问题介绍 #

直线分隔问题是在数学中常见的一种问题，首先由直线划分区域到折线划分区域，再延伸到封闭图形划分区域，最后在推广为平面划分空间的问题。
以直线为例，对直线分隔问题进行分析。
问题可概述如下：
n条直线，最多可以把平面分为多少个区域？

直线分隔问题分析 #

假设有n-1条直线时，平面最多被分成了f（n-1）个区域。第n条直线要是切成的区域数最多，就必须与之前的（n-1）条直线都相交且不能有同一交点。 这样就会得到（n-1）个交点。
这些交点将第n条直线分为2条射线和n-2条线段。而每条射线和线断将以有的区域一分为二。这样就多出了2+（n-2）个区域。
故可以得出递推公式：f(n)=f(n-1)+n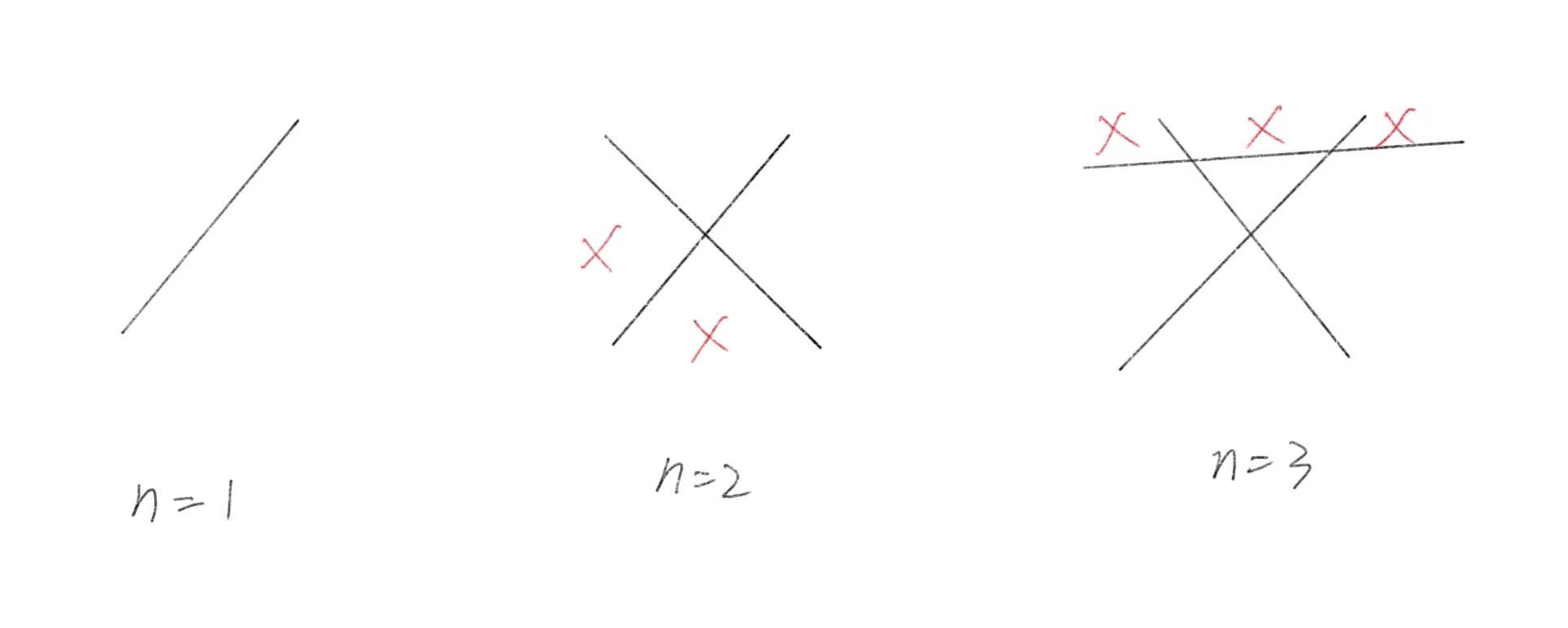

直线分隔问题的实现 #

python实现代码如下：

def line_surface(n):
    if n==1:
        return 2
    return line_surface(n-1)+n #每多一条直线，比第（n-1）条直线时多出来n个平面


if __name__=='__main__':
    print(line_surface(10))

小结 #

理解并掌握直线分隔问题的思想
掌握直线分隔问题的代码实现

习题 #

1. 习题1：画出直线分隔问题的流程图
2. 习题2：当存在587条直线时，最多可以将平面分割成多少区域？