平面分隔问题2——封闭曲线分隔 #

1. 封闭曲线分隔问题介绍
2. 封闭曲线分隔问题分析
3. 封闭曲线分隔问题的实现

收获 #

学完本节内容，可以初步理解并掌握封闭曲线分隔问题的原理及实现。

封闭曲线分隔问题介绍 #

封闭曲线分隔问题是在数学中常见的一种问题，这里的封闭曲线常常指的是圆。
问题可概述如下：
n个圆，最多可以把平面分为多少个区域？

封闭曲线分隔问题分析 #

当n-1个圆时，区域数为f(n-1).那么第n个圆就必须与前n-1个圆相交，则第n个圆被分为2（n-1）段线段，增加了2（n-1）个区域。
故可以得出递推公式： f(n)=f(n-1)+2(n-1)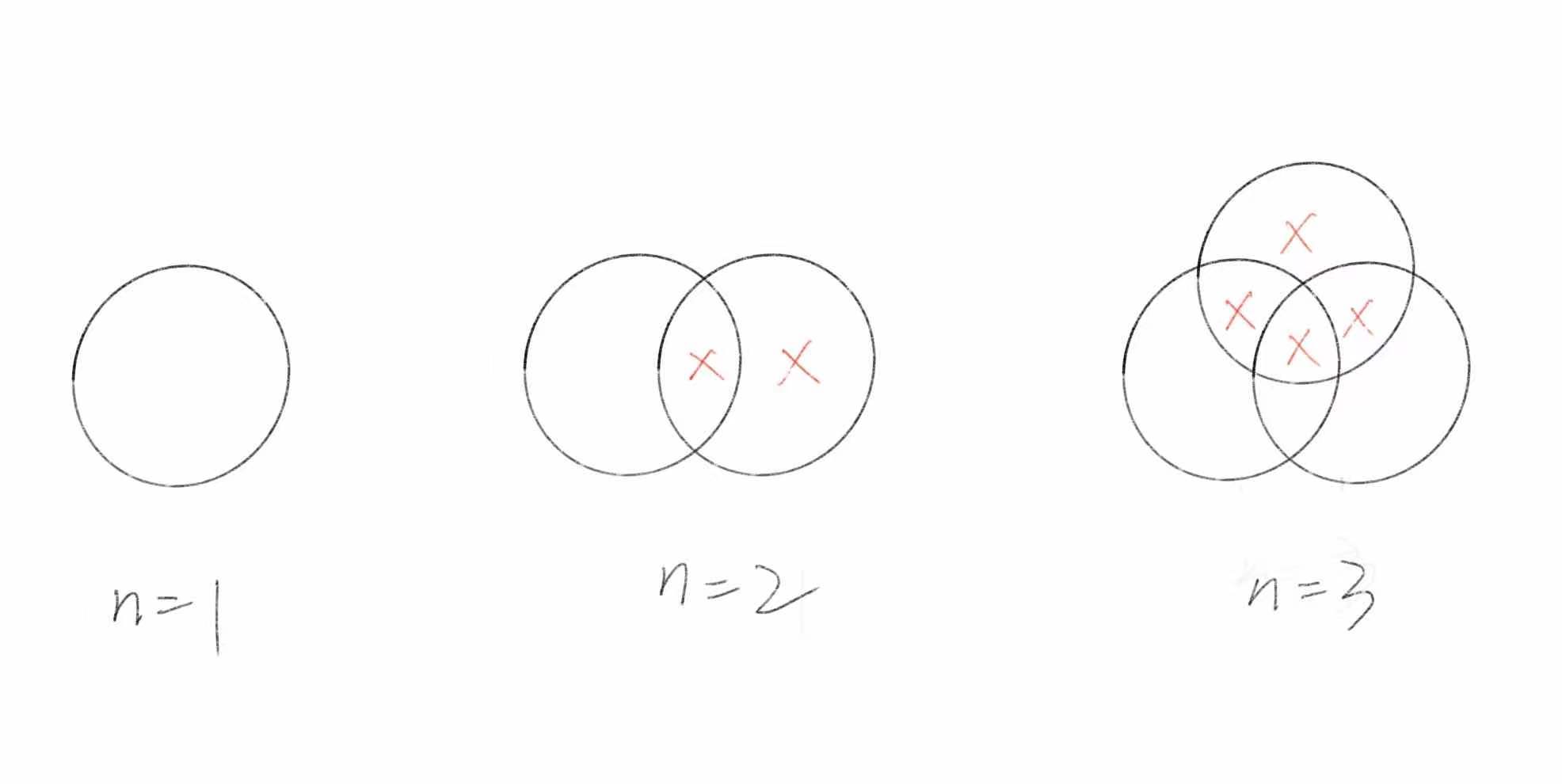

封闭曲线分隔问题的实现 #

python实现代码如下：

#封闭曲线（圆）分隔问题
def circle_surface(n):
    if n==1:
        return 2
    return circle_surface(n-1)+2*(n-1)

if __name__=='__main__':
    print((circle_surface(10)))

小结 #

理解并掌握封闭曲线分隔问题的思想
掌握封闭曲线分隔问题的代码实现

习题 #

1. 习题1：画出封闭曲线分隔问题的流程图
2. 习题2：当存在58个圆时，最多可以将平面分割成多少区域？