回溯算法2 #

1. 回溯算法解决的问题
2. 回溯算法的的理解1
3. 回溯算法的的理解2

回溯算法解决的问题 #

回溯法能够解决的问题，都能够抽象为一颗树的结构。就绘画一颗树一样，从树的枝干出发，到树杈一直到树叶，就画成了一颗树的一条路径。

回溯算法的的理解1 #

在求解{‘a’,’b’,’c’}三个字母的排列问题时，我们用一个树形的结构来求解问题的步骤如下:

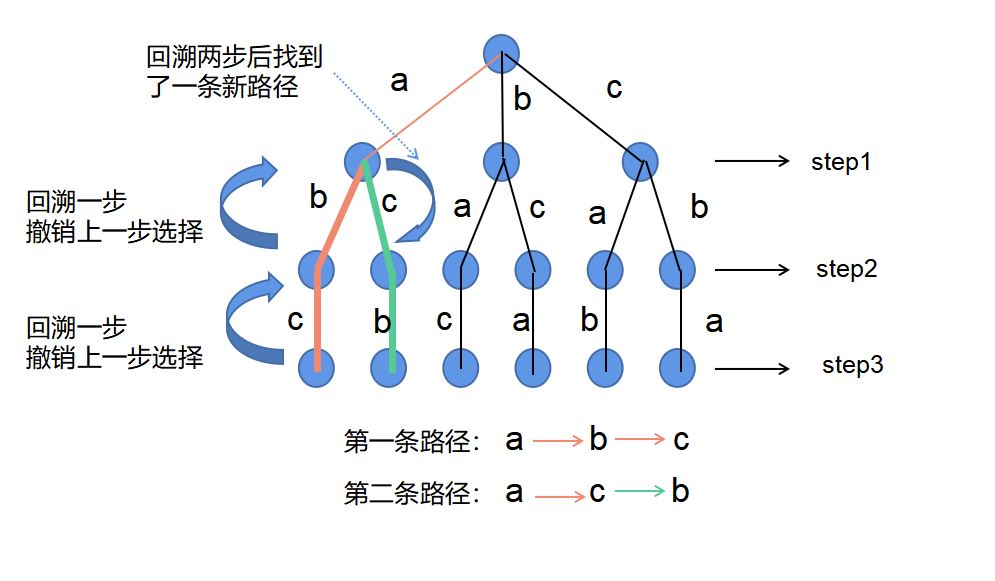
在求解上述问题时我们分为了三步:
step1：从’a’,’b’,’c’三个字母中选取一个，作为排列的第一个字母
step2：从以第一个字母为基准，从剩下的两个字母择一选择
step3：以前两个字母选择为基准，选择最后一个字母

s=['a','b','c'] #需要排列的一个集合，我们使用列表来表示
res=[0]*3 #排列问题每一步的结果
status=[True]*3 #定义一个状态列表，True表示对应列表S索引的字母能够选择，False表示对应列表S索引的字母不能够被选择
def dfs(step): #定义回溯函数dfs(step),step代表了每一步，也是递归的深度
    if step>3: #已经完成了3步，说明解决问题的一条路径已经完成，输出结果
        print(res)
        return
    for i ,char in enumerate(s): #从{a,b,c}中选取一个，存放到结果列表中
        if(status[i]): #判断当前的字母能否被选择，不能被选择函数执行完毕
            res[step-1]=char #将每一步选择的字母，存放到结果列表中
            status[i]=False #在进行下一步选择字母之前，把当前选择的字母状态变在下一步变为不可选择，避免选择重复的字母
            dfs(step+1) #寻找下一步的可行选择
            status[i]=True #寻找下一步结束，回溯执行时，把当前的字母状态撤销 ，避免上一步无法对当前选择的字母进行选择
dfs(1)

回溯算法的的理解2 #

在求解{‘a’,’b’,’c’}的有多少个子集问题时，我们同样分成三步:
step1:使用path[0]来记录第一个元素a，是否被选择 (1代表选择，0代表未选择)。
step2:使用path[1]来记录第二个元素b，是否被选择。
step3:使用path[2]来记录第三个元素c，是否被选择。
使用回溯算法思想，将所有的可能情况都一一列举，就能得到{a,b,c}所有的子集

s=['a','b','c'] #需要求解子集的集合，我们使用列表来表示
path=[0]*3 #定义一个路径列表，按照索引对应列表s中的每个元素，1代表选择，0代表未选择
res=[] #存储最后的结果
def myprint(): #定义打印结果的函数
    print('path=',path, end=' ')
    res = [s[i] for i in range(len(path)) if (path[i])]
    print('res=',res)
    res.clear()
def dfs(step): #定义回溯函数dfs(step),step代表了每一步，也是递归的深度
    if(step>3):
        myprint()
        return
    path[step-1]=0 #当前路径选择0
    dfs(step+1)#递归寻找下一步
    path[step-1]=1 #当前路径选择1(该步是对path[step-1]=0选择的撤销，回溯的目的就是把当前所有可能的选择都尝试一遍)
    dfs(step+1)#递归寻找下一步(因为当前所有的选择，只能是0和1，回溯后无需再执行其它操作，函数结束)
dfs(1)

小结 #

习题 #

1. 上述两个问题都能够使用循环去解决，试用循环的方法求解集合{‘a’,’b’,’c’}的排列问题以及子集问题？
2. 对于集合元素较多的集合，如{‘a’,’b’,’c’,’d’,’e’,’f’,’g’,’h’}的排列问题以及子集问题，如果还使用循环解决会发生什么情况？
3. 根据回溯算法理解2的代码，画出解决{a,b,c}子集问题的树状结构图，并求解{‘a’,’b’,’c’,’d’,’e’,’f’,’g’,’h’}的子集个数