跳至正文
View Categories

< 1 min read

效益问题 #

  1. 效益问题的介绍
  2. 效益问题的算法分析
  3. 效益问题代码实现

效益问题的介绍 #

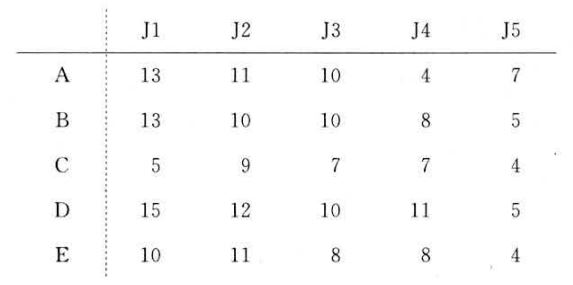
假设有A、B、C、D、E五人从事J1,J2,J3,J4,J5五项工作，每人只能从事一项，如果使得他们的效益之和最高，他们的效益图如下:

效益问题的算法分析 #

如果使用1，2，3，4，5分别来表示J1,J2,J3,J4,J5,那么上述问题其实就变成了一个1，2，3，4，5的排列问题，即在A( ),B( ),C( ),D( ),E( )的括号中，填入合适的1，2，3，4，5排列使得效益值最大。利用回溯法求出上述所有排列，再求效益最大即可。

效益问题的代码实现 #

data=[[13,11,10,4,7],
      [13,10,10,8,5],
      [5,9,7,7,4],
      [15,12,10,11,5],
      [10,11,8,8,4]]#记录A,B,C,D,E做某件工作的效益
sum=0;#表示总效益
job=[1,2,3,4,5]#1，2，3，4，5表示j1,j2,j3,j4,j5
res=[0]#索引1的值表示A选择的结果,索引2表示B选择的结果以此类推
s=[True]*6#s[1]=True表示job1可以选择以此类推
def dfs(step):
    if(step>5):
        sum1=0
        for i in range(1,6):#求解每个排列的效益A对应行，j1对应列以此类推
            sum1=sum1+data[i-1][res[i]-1]
        global sum
        if(sum<sum1):#如果效益比上一步大更新sum结果
            sum = sum1
            print(res[1:],"max=%d"%(sum))
        return
    for i in job: #从1，2，3，4，5选取一个数
        if s[i]==True: 
            res.append(i)#如果该数字可以选保留结果
            s[i]=False #下一步该数不能再选，以免重复
            dfs(step+1)#寻找下一步结果
            s[i]=True#回溯后保存之前的状态
            res.pop()
dfs(1)从第一步开始求解

小结 #

  • 根据效益问题，理解回溯算法在排列中的应用
  • 掌握效益问题求解的回溯算法

习题 #

  1. 如果在上述问题中，因为一些原因A不能选择工作J5,其余条件不变求解效益问题的最大值
  2. 试求出上述问题一共有多少种选择，并求出所有选择当中的效益最小值
What are your Feelings