迷宫问题 #

1. 迷宫问题问题的介绍
2. 迷宫问题问题的算法分析
3. 迷宫问题问题代码实现

迷宫问题问题的介绍 #

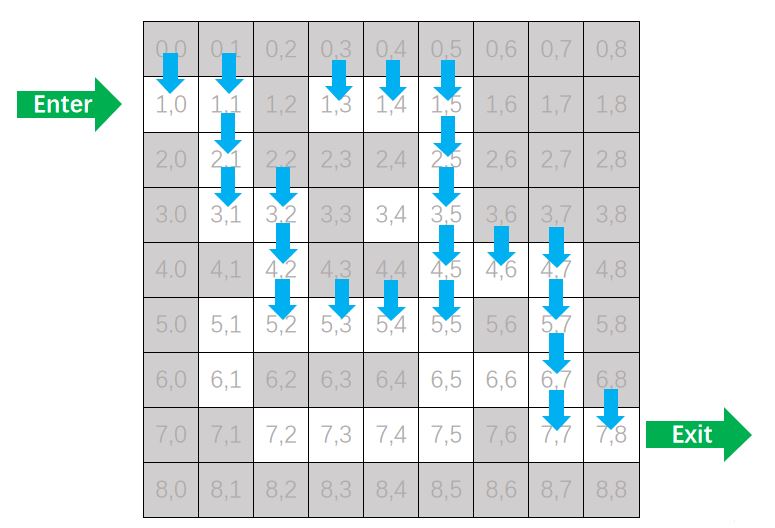
迷宫问题是典型的回溯问题，如下图的迷宫入口处在坐标的 (1，0) 出口在 (7，8)处，迷宫中黑色的部分代表是障碍物不能通过，进入迷宫的人每次只能朝四个方向没有障碍物的方向移动一步。

迷宫问题问题的算法分析 #

迷宫问题问题与跳马问题类似，不同之处在于，迷宫中有较多的障碍物，假设(x,y)表示人当前所处的位置，则下一次的移动轨迹只可能又如下四步(x表示横坐标，也表示纵坐标):
(x,y)->(x+1,y)
(x,y)->(x-1,y)
(x,y)->(x,y+1)
(x,y)->(x,y-1)
第一步:从(1,0)处出发，判断是否到达了迷宫出口，如果不是朝着一个可能的移动方向移动，记录结果，并将移动的轨迹做标记，防止下一步退回原地。
第二步:如果进入死胡同就后退一步，朝着一个另外可能的移动方向移动，一直到达迷宫出口

迷宫问题问题的代码实现 #

maze=[#迷宫的状态矩阵，0代表不能通过，1代表能通过
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 1, 1, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 1, 0, 0, 0],
[0, 0, 1, 0, 0, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0, 1, 0],
[0, 1, 0, 0, 0, 1, 1, 1, 0],
[0, 0, 1, 1, 1, 1, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0],]
res=[[1,0]]#[1,0]是迷宫的入口,作为初始的选择
maze[1][0]=0#将已经走过每一步,做上标记,下一步不能被选择
d=[[1,0],[-1,0],[0,1],[0,-1]]#迷宫中人的四种移动轨迹
def myprint(r):#按要求打印结果
    for i in r:
        print(i,'->',sep='',end='')
    print('\b\b')
def dfs(step):
    if res[step-1]==[7,8]:#如果上一步选择已经到达终点打印结果
        myprint(res)
        return
    for i in d:
        if(maze[res[step-1][0]+i[0]][res[step-1][1]+i[1]]):
            [x,y]=[res[step-1][0]+i[0],res[step-1][1]+i[1]]
            maze[x][y]=0
            res.append([x,y])#保留结果
            dfs(step+1)#寻找下一步
            res.pop()#撤销当前的选择
            maze[x][y]=1
dfs(1)#从第一步开始寻找迷宫的出路

小结 #

• 根据迷宫问题问题，理解回溯算法试探法的含义
• 掌握迷宫问题求解的回溯算法

习题 #

1. 如果在迷宫问题中，maze矩阵的索引[4,8]处也是出口，试求解所有的路径
2. 如果在迷宫问题中每一步选择的结果不做标记，会发生什么情况？