递归与回溯算法的总结 #

1. 递归及回溯算法的概念
2. 递归及回溯算法的理解
3. 递归及回溯算法的算法思想

递归以及回溯算法的概念 #

递归:函数自己调用自己。自己调用自己这个特性，有一种自动化的力量，给它一个规则，它可以自动的持续运行下去，直到触发停止条件。
回溯:本层函数结束后，回到上一步。它是递归的副产物，递归触发停止条件后就会回到上一步。
回溯算法:如果在递归调用结束之后，能够撤销当前的选择，再回到上一步继续递归，就变成了试探法，也就是回溯算法。

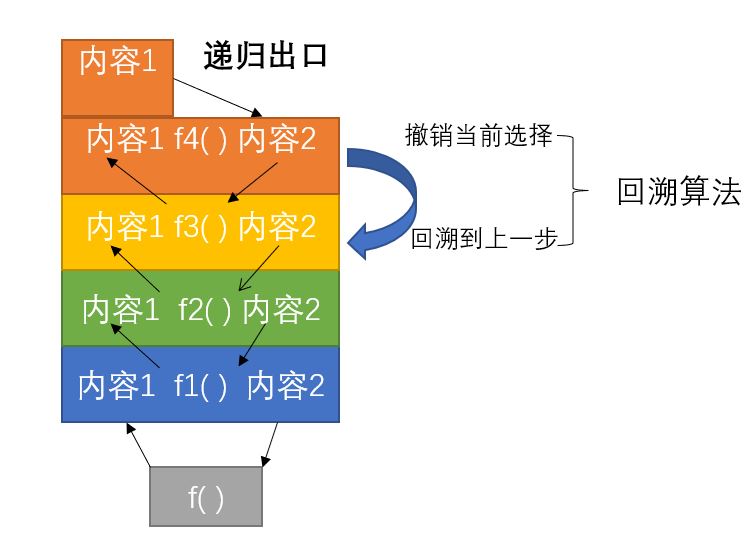
递归及回溯的理解 #

在递归263课的讲解中我们讲解了，求解n!的递归写法，当 n<=5 时，下面的f(),f1(),f2(),f3(),f4()的定义模拟了递归函数的执行过程。
从f4()-> f3()-> f2()-> f1()-> f()则模拟了递归调用中的回溯过程。

def f(n):#输入n的参数满足n<=5
    if(n==1):
        return 1
    s=n*f1(n-1)
    print(s)
    return s
def f1(n):#输入n的参数满足n<=4
    if (n == 1):
        return 1
    s=n*f2(n-1)
    print(s)
    return s
def f2(n):#输入n的参数满足n<=3
    if (n == 1):
        return 1
    s=n*f3(n-1)
    print(s)
    return s
def f3(n):#输入n的参数满足n<=2
    if (n == 1):
        return 1
    s=n*f4(n-1)
    print(s)
    return s
def f4(n):#输入n的参数满足n<=1
    if (n == 1):
        return 1
f(5)

递归及回溯算法的算法思想 #

递归的思想：把问题分解成为规模更小的、具有与原问题有着相同解法的问题。
回溯算法的思想：利用递归回溯特新的试探法，是有限制条件的穷举法。
递归以及回溯解决的典型问题类型:
1.能归纳出递归表达式的数学问题(递归)
2.汉诺塔、波兰表达式(递归)
3.(有限制条件的)排列问题(回溯算法)
4.(有限制条件的)集合问题(回溯算法)
5.(有限制条件的)棋盘问题(回溯算法)

小结 #

• 递归以及回溯算法的总结
• 能够理解递归函数的调用和回溯过程，理解回溯算法是如何利用递归实现试探的

习题 #