活动选择1 #

1. 活动选择问题的介绍
2. 活动选择问题的算法分析
3. 活动选择问题代码实现

活动选择问题的介绍 #

学校活动中心周日将面向全校各个学院的学生社团开放，但活动中心同时只能供一个社团活动使用，并且每一个社团活动开始后都不能中断。现在各个社团都提交了他们使用该中心的活动计划（即活动的开始时刻和截止时刻）。请设计一个算法来找到一个最佳的分配序列，以能够尽可能多的安排社团活动。
比如有11个活动，开始与截止时刻如下图(Si开始时间，fi结束时间)：

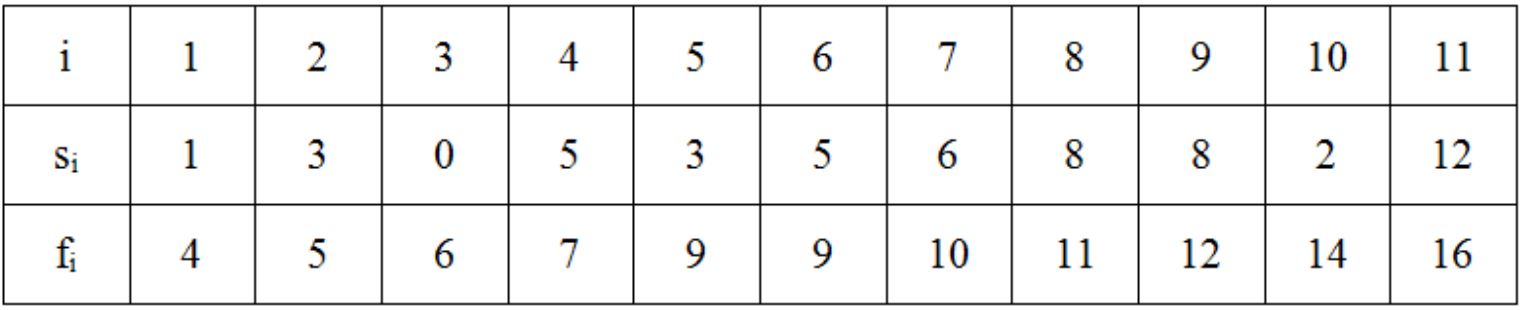
活动选择问题的算法分析 #

画出每一个活动的时间如下图，关于活动选择问题贪心策略的选择，很容易想到的有以下几种

• 1)每一次从不冲突的活动中，选择开始时间最早的
• 2)每一次从不冲突的活动中，选择活动时最短的
• 3)每一次从不冲突的活动中，选择结束时间最早的

对于上述的三种贪心策略：

• 1)能够很容易举出反例，如果一个活动开始时间很早，但是活动时间很长，甚至占据了整天的时间，那么选择该活动是不恰当的。
• 2)符合一部分人的想法，而且在本例中使用能够安排活动2、活动4、活动8、活动11四个活动，与使用贪心策略3安排活动数目相同。但是当很短时间的活动占据比较关键的位置时，可能会导致该策略的失效例如下图：
  
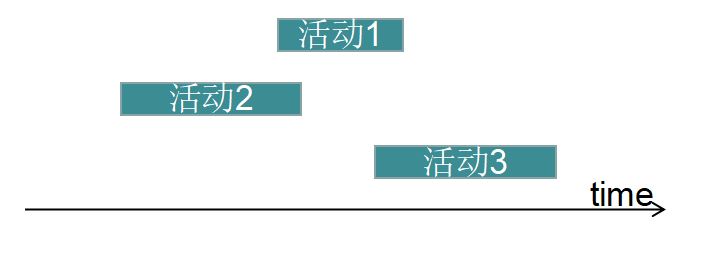
  很容易可以看到如果选择最短时间的活动1的话，将会导致活动2以及活动3均不能选。
• 3)按照此策略，如上图我们可以选择活动1、活动2、活动4、活动11四个活动，对于本例选择的过程如下图所示:
  
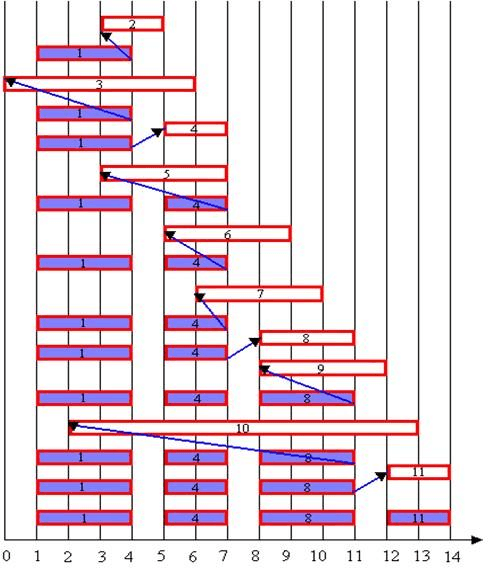
  首先选择结束活动最早的活动1，再余下的活动中选择与活动1不冲突的活动4，以此类推

小结 #

• 根据活动选择问题，理解贪心算法
• 掌握活动选择问题策略的制定，能够结合实际问题作出合适的贪心策略

习题 #

1. 1)有人说贪心算法没有固定的套路，就是常识性推导加上举反例，谈一谈你对本句话的理解
2. 2)根据283课贪心算法2的讲解，尝试证明本例中贪心策略3)的可行性？