跳至正文
View Categories

< 1 min read

活动选择2 #

  1. 活动选择问题的贪心可行性证明
  2. 活动选择问题代码实现

活动选择问题的可行性证明 #

在283课贪心算法2的讲解中，我们提到了证明贪心算法可行性分为两步:

  • 1）首先证明存在一个最优解，该最优解是以贪心策略选择开始:

    对于上图中的问题，首先我们假设活动选择问题存在一个最优解S，可以安排n个活动，S中的活动按照最早结束时间排列为{S1,S2,S3……Sn}
    在上图中活动1的结束时间最短，因此活动1的结束时间早于或等于S1，即f1<=fs1,因此如果{S1,S2,S3……Sn}是原问题的最优解，那么{活动1，S2,S3……Sn}也是原问题的最优解:

    那么该问题就存在一个，以最早时间结束为策略，开始的最优解{活动1，S2,S3……Sn},可以安排n个活动。
  • 2）其次证明该问题具有最优子结构:
    以贪心策略选择活动1后，那么原问题就转化为在活动1结束时间之后，即在时间段4~14中尽可能多的安排活动。那么我们我们只需证明其子结构{S2,S3……Sn}是该子问题的最优解即可。这是十分明显的，使用反证法：
    如果{S2,S3……Sn}不是该问题的最优解，即能够在4~14时间段中找到更多的活动{V2,V3,V4……Vm} (m>n-1), 那么{活动1,V2,V3,V4……Vm} (m+1>n) ，是原问题的解。该解的个数已经大于n，与原问题最优解可以安排n个活动矛盾。因此活动区间问题具有最优子结构。
    因为结合一二步就可以证明，活动区间问题的贪心策略是可行的，大家熟悉上述证明方法即可，不要求掌握。

    活动选择问题的代码实现 #

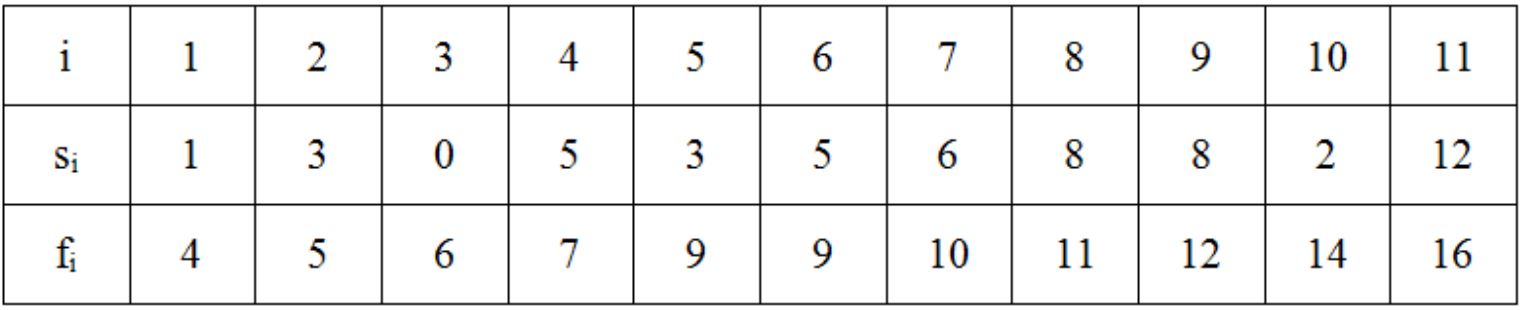
    res=[1]#保留每步结果,首先选活动1
s=[0]+[1,3,0,5,3,5,6,8,8,2,12]#将活动按照结束时间从小到大排序,s[1]表示活动1以此类推
f=[0]+[4,5,6,7,9,9,10,11,12,14,16]
n=11
for i in range(2,n+1):#从活动2开始选，依次类推
    if s[i]>f[res[-1]]:#当前活动与之前最后结束的活动不冲突
        res.append(i)
print(res)#打印结果

    小结 #

    • 根据活动选择问题贪心可行性的证明，了解贪心可行性证明的方法
    • 掌握活动选择问题的贪心算法，理解具体问题具有最优子结构的含义

    习题 #

    1. 1)活动选择问题的贪心算法是可行的，结合本例找一找有没有其他选择，也能够安排4个活动？
    2. 2)能使用回溯法对该问题进行求解吗？和回溯相比贪心有什么优点？
What are your Feelings