树 #

1. 树的定义
2. 树的基本概念
3. 树的种类

树的定义 #

1. 在学习数这种数据结构之前，我们学习了栈、队列、链表总得来说它们都属于线性表，存储方式上有顺序存储的线性表，也有链式存储的线性表，根据具体需要构建相应数据结构
2. 一颗数是由n个元素组成的一种非线性数据结构，每个元素我们通常称为结点(node)
3. 有一个特定的结点， 称为根结点或树根(root)
4. 除根结点外，其余结点能分成 m(m>=0)个互不相交的有限集合 T0,T1,……Tm-1,其中的每个子集又是一棵树,这些数称为这棵树的子树

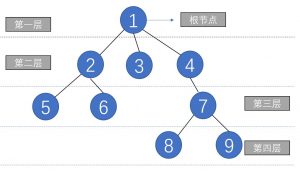
树的基本概念 #

1. 树是递归定义的，每个元素称为结点(node),有一个特定的结点被称为根结点或树根(root),除根结点之外的其余数据元素被分为m(m≥0)个互不相交的结合T1，T2，……Tm-1，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）
2. 一棵树中至少有 1 个结点(也有定义空集合也是树，空树中没有节点)。这个结点就是根结点，没有前驱，其余每个结点都有唯一的一个前驱结点
3. 一个结点的子树个数,称为这个结点的度(结点1的度为 3,结点3的度为0);度为0的结点称为叶结点;度不为0的结点称为分支结点;树中各结点的度的最大值称为这棵树的度
4. 在用图形表示的树型结构中，对两个用线段(称为树枝)连接的相关联的结点，称上端结点为下端结点的父结点或双亲节点，称下端结点为上端结点的子结点。称同一个父结点的多个子结点为兄弟结点。称从根结点到某个子结点所经过的所有结点为这个子结点的祖先。称以某个结点为根的子树中的任一结点都是该结点的子孙
5. 定义一棵树的根结点的层次(level)为 0,其他结点的层次等于它的父结点层次加 1，一棵树中所有的结点的层次的最大值称为树的深度(depth)或高度
6. 对于树中任意两个不同的结点，如果从一个结点出发，自上而下沿着树中连着结点的线段能到达另一结点， 称它们之间存在着一条路径，结点1和结点8之间存在着一条路径，并用(1、4、7、8)表示这条路径.该条路径的长度3。不同子树上的结点之间不存在路径，从根结点岀发，到树中的其余结点一定存在着一条路径
7. 森林(forest)是 m( m>=0 )棵互不相交的树的集合

树的表示方法 #

1. 图形表示法:上图就是使用图形表示法，参考树的基本概念
2. 符号表达法:用括号先将根结点放入一对圆括号中，然后把它的子树由左至右的顺序放入括号中，而对子树也采用同样的方法处理；同层子树与它的根结点用圆括号括起来，同层子树之间用逗号隔开，最后用闭括号括起来。如前文树形表示法可以表示为：(1(2(5,6),3,4(7(8,9))))
3. 遍历表达法:如上述树使用层次遍历方法表示为(1,2,3,4,5,6,7,8,9),另有中序遍历、后续遍历、前序遍历后续做出说明

小结 #

1. 理解树的定义
2. 掌握数的基本概念
3. 掌握数的表示方法

习题 #

1. 找出上图树中的叶节点，以及树的深度，想一想树的深度与最大路径长度的关系
2. 谈一谈你对树递归定义的了解，并标出上述树中每个节点的度以及它的双亲节点