主要内容 #
- 算法讲解
- 例程
- 复杂度分析
1. 算法讲解 #
选择排序(Selection sort)是一种简单直观的排序算法。
它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
过程模拟:(请大家观察下面的排序过程,并总结排序规律)
原始数据 [49 38 65 97 76 13 27 49] 第1次排序 13 [49 38 65 97 76 27 49] 第2次排序 13 27 [49 38 65 97 76 49] 第3次排序 13 27 38 [49 65 97 76 49] 第4次排序 13 27 38 49 [65 97 76 49] 第5次排序 13 27 38 49 49 [65 97 76] 第6次排序 13 27 38 49 49 65 [97 76] 第7次排序 13 27 38 49 49 65 97 [76] 结束排序
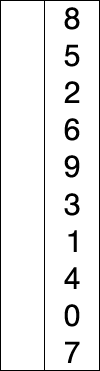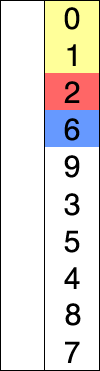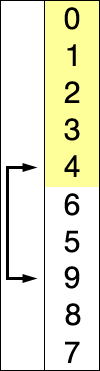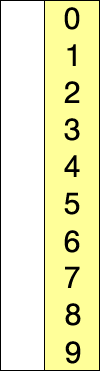
红色表示当前最小值,黄色表示已排序序列,蓝色表示当前位置。
2. 例程 #
请将上述的过程用代码写出来。
示例程序:
#include < iostream >
using namespace std;
int main()
{
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
int n = sizeof(a)/sizeof(int); // 计算数组的长度
for (int i = 0; i < n; ++i)
{
int k = i;
for (int j = i + 1; j < n; ++j)//走访未排序的元素
if (a[j] < a[k]) // 找到目前最小值
k = j; //记录最小值
if (k != i) // 交换两个元素
{
int temp = a[i];
a[i] = a[k];
a[k] = temp;
}
}
for (int i = 0; i < n; ++i)
cout << a[i] << " ";
return 0;
}
3. 复杂度分析 #
选择排序的交换操作介于0和(n-1)次之间。选择排序的比较操作为n(n-1)/2次。选择排序的赋值操作介于3(n-1)次之间。在最好情况下也就是数组完全有序的时候,无需任何交换移动,在最差情况下,也就是数组倒序的时候,交换次数为n-1次。综合下来,时间复杂度为O(n*n)
习题 #
请默写上述代码。




