主要内容 #
- 算法讲解
- 例程
- 复杂度分析
1. 算法讲解 #
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢”浮”到数列的顶端。
1.1 计算步骤 #
1. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤,除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
1.2 过程模拟 #
原始数据 [ 49 38 65 97 76 13 27 49 ]
第1次排序 [(38__49) 65 97 76 13 27 49 ] // AA__BB 表示数字发生了交换
[ 38 (49 65) 97 76 13 27 49 ]
[ 38 49 (65 97) 76 13 27 49 ]
[ 38 49 65 (76__97) 13 27 49 ]
[ 38 49 65 76 (13__96) 27 49 ]
[ 38 49 65 76 13 (27__96) 49 ]
[ 38 49 65 76 13 27 (49__96)] // 最大值 96 已经移动到了最右边
第2次排序 [(38 49) 65 76 13 27 49 96 ]
[ 38 (49 65) 76 13 27 49 96 ]
[ 38 49 (65 76) 13 27 49 96 ]
[ 38 49 65 (13__76) 27 49 96 ]
[ 38 49 65 13 (27__76) 49 96 ]
[ 38 49 65 13 27 (49__67) 96 ] // 第 2 大值 67 已经找到了
[ 38 49 65 13 27 49 (67 96)] // 可以省略
第3次排序 [(38 49) 65 13 27 49 67 96 ]
[ 38 (49 65) 13 27 49 67 96 ]
[ 38 49 (13__65) 27 49 67 96 ]
[ 38 49 13 (27__65) 49 67 96 ]
[ 38 49 13 27 (49__64) 67 96 ] // 第 3 大值 64 已经找到了
[ 38 49 13 27 49 (64 67) 96 ] // 可以省略
[ 38 49 13 27 49 64 (67 96)] // 可以省略
第4次排序 [(38 49) 13 27 49 64 67 96 ]
[ 38 (13__49) 27 49 64 67 96 ]
[ 38 13 (27__49) 49 64 67 96 ]
[ 38 13 27 (49 49) 64 67 96 ] // 第 4 大值 49 已经找到了
[ 38 13 27 49 (49 64) 67 96 ] // 可以省略
[ 38 13 27 49 49 (64 67) 96 ] // 可以省略
[ 38 13 27 49 49 64 (67 96)] // 可以省略
第5次排序 [(13__38) 27 49 49 64 67 96 ]
[ 13 (27__38) 49 49 64 67 96 ]
[ 13 27 (38 49) 49 64 67 96 ] // 第 5 大值 49 已经找到了
[ 13 27 38 (49 49) 64 67 96 ] // 可以省略
[ 13 27 38 49 (49 64) 67 96 ] // 可以省略
[ 13 27 38 49 49 (64 67) 96 ] // 可以省略
[ 13 27 38 49 49 64 (67 96)] // 可以省略
第6次排序 [(13 27) 38 49 49 64 67 96 ]
[ 13 (27 38) 49 49 64 67 96 ] // 第 6 大值 38 已经找到了。(其实到这里排序就可以结束,循环到n-2次)
[ 13 27 (38 49) 49 64 67 96 ] // 可以省略
[ 13 27 38 (49 49) 64 67 96 ] // 可以省略
[ 13 27 38 49 (49 64) 67 96 ] // 可以省略
[ 13 27 38 49 49 (64 67) 96 ] // 可以省略
[ 13 27 38 49 49 64 (67 96)] // 可以省略
第7次排序 [(13 27) 38 49 49 64 67 96 ] // 第 7 大值 27 已经找到了,且第 8 大值 13 也已经确定
[ 13 (27 38) 49 49 64 67 96 ] // 可以省略
[ 13 27 (38 49) 49 64 67 96 ] // 可以省略
[ 13 27 38 (49 49) 64 67 96 ] // 可以省略
[ 13 27 38 49 (49 64) 67 96 ] // 可以省略
[ 13 27 38 49 49 (64 67) 96 ] // 可以省略
[ 13 27 38 49 49 64 (67 96)] // 可以省略
第8次排序 [(13 27) 38 49 49 64 67 96 ] // 可以省略,第 8 大值 13 已经确定
[ 13 (27 38) 49 49 64 67 96 ] // 可以省略
[ 13 27 (38 49) 49 64 67 96 ] // 可以省略
[ 13 27 38 (49 49) 64 67 96 ] // 可以省略
[ 13 27 38 49 (49 64) 67 96 ] // 可以省略
[ 13 27 38 49 49 (64 67) 96 ] // 可以省略
[ 13 27 38 49 49 64 (67 96)] // 可以省略
结束排序
动画演示如下图所示:
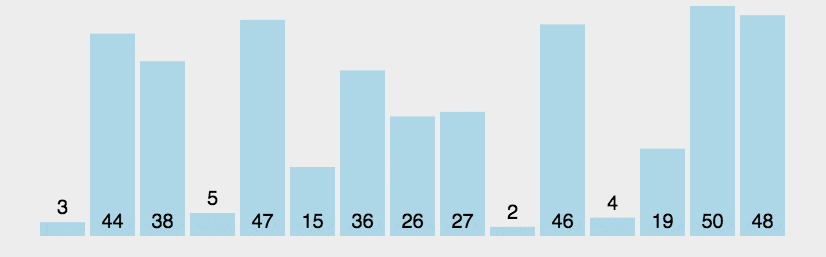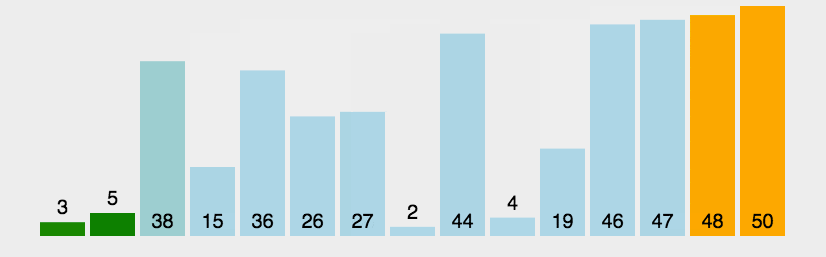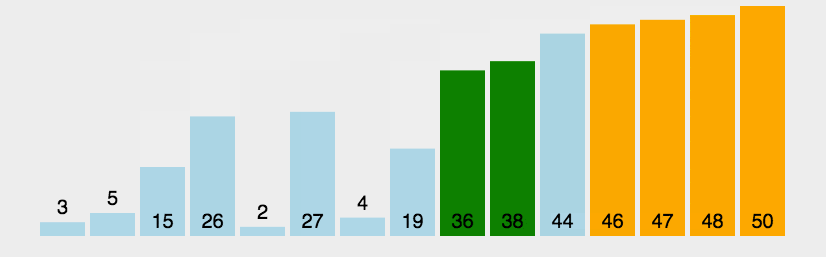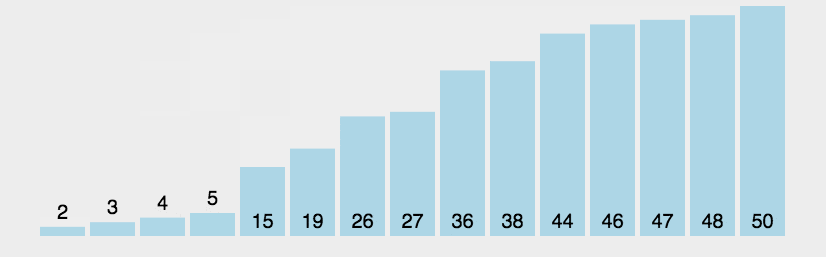
2. 例程 #
请将上述的过程写出来。
示例程序:
#include < iostream >
using namespace std;
int main()
{
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
int n = sizeof(a)/sizeof(int); // 请解释这段代码的意义
for (int i = 0; i < n; ++i) // 请问可以优化吗?(提示:i < n 可优化)
{
for (int j = 0; j < n-1; ++j)
{
if (a[j] > a[j+1])
swap(a[j], a[j+1]); // 如何自己实现?
}
}
for (int i = 0; i < n; ++i)
cout << a[i] << " ";
return 0;
}
3. 复杂度分析 #
请问,这两个排序方法分别进行了多少次【比较】操作?你认为谁的速度快?
冒泡排序是与插入排序拥有相等的渐近时间复杂度,但是两种算法在需要的交换次数却很大地不同。
在最坏的情况,冒泡排序需要O(n^2)次交换,而插入排序只要最多O(n)交换。冒泡排序的实现通常会对已经排序好的数列拙劣地执行O(n^2)),而插入排序在这个例子只需要O(n)个运算。因此很多现代的算法教科书避免使用冒泡排序,而用插入排序取代。
习题 #
请默写上述代码。(优化答案:i < n 可以改为 i < n-2)




