主要内容 #
- 算法讲解
- 例程
- 复杂度分析
1. 算法讲解 #
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高!它是处理大数据最快的排序算法之一了。
1.1 计算步骤 #
一般来说,具体算法描述如下:
1. 挑选基准值:从数列中挑出一个元素,称为“基准”(pivot),
2. 分割:重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(与基准值相等的数可以到任何一边)。在这个分割结束之后,对基准值的排序就已经完成,
3. 递归排序子序列:递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。
递归到最底部的判断条件是数列的大小是零或一,此时该数列显然已经有序。
1.2过程模拟 #
原始数据:int a[] = {49,38,65,97,76,13,27,49};
l---------------------------r // l 表示最左边的数的序号;r 表示最右边的数的序号
49 38 65 97 76 13 27 49
过程分析:
1. 找出数组中间的数,76
l---------------------------r
[ 49 38 65 97 (76) 13 27 49]
2. 从【左边】开始查找【第一个大于】 76 的数,用 i 记录,见 i97
l-----------i---------------r
[ 49 38 65 97 (76) 13 27 49]
3. 从【右边】开始查找【第一个小于】 76 的数,用 j 记录,见 j49
l-----------i---------------jr // jr 表示在这里就 j 和 r 相同
[ 49 38 65 97 (76) 13 27 49]
4. 判断是否要交换 i97 和 j49。【判断条件 1: a[i] > [j]】;【判断条件 2: i <= j】。
l-----------i---------------jr
[ 49 38 65 49 (76) 13 27 97] // 2 个条件都成立,所以交换 i97 和 j49
5. i++;j--;
l---------------i-------j---r
[ 49 38 65 49 (76) 13 27 97]
6. 继续步骤 2、3,找到 j27 i97,步骤 4 中的条件不成立,不交换
l-----------------------j---r
[ 49 38 65 49 (76) 13 27 97]
7. 循环条件【i<=j】不成立。分成 2 个数组,序号范围分别是 l~j,i~r
l-----------------------j---ir // ir 在这里相同,都是 97 的序号
[ 49 38 65 49 (76) 13 27 97]
|
\|/
[ 49 38 65 49 76 13 27][97]
8. 分别对两个数组,继续进行步骤 1-7 的操作。
8.1 先看左边的,取中间数 49
l------------------------r // 这里的 lr 要理解成递归调用中的l和r,表示数组范围
[ 49 38 65 (49) 76 13 27]
8.2 从【左边】开始查找【第一个大于】 49 的数,用 i 记录,见 i65
l-------i----------------r
[ 49 38 65 (49) 76 13 27]
8.3 从【右边】开始查找【第一个小于】 49 的数,用 j 记录,见 j27
l-------i----------------jr
[ 49 38 65 (49) 76 13 27]
8.4 判断是否要交换 i65 和 j27。【判断条件 1: a[i] > [j]】;【判断条件 2: i <= j】。
l-------i----------------jr
[ 49 38 27 (49) 76 13 65] // 2 个条件都成立,所以交换
8.5 i++;j--;
l-----------i--------j---r
[ 49 38 27 (49) 76 13 65]
8.6 继续步骤 2、3,找到 i76 和 j13
l----------------i---j---r
[ 49 38 27 (49) 76 13 65]
8.7 【判断条件 1: a[i] > [j]】;【判断条件 2: i <= j】
l----------------i---j---r
[ 49 38 27 (49) 13 76 65] // 2 个条件都成立,所以交换
8.8 i++;j--;
l----------------j---i---r
[ 49 38 27 (49) 13 76 65] // 2 个条件都成立,所以交换
8.9 循环条件【i<=j】不成立。分成 2 个数组,序号范围分别是 l~j,i~r
l----------------j---i---r
[ 49 38 27 49 13][76 65]
********** 请试着补全后续操作步骤 *******
最终:
[ 13 27 38 49 49 65 76 97 ]
动画演示如下图所示:
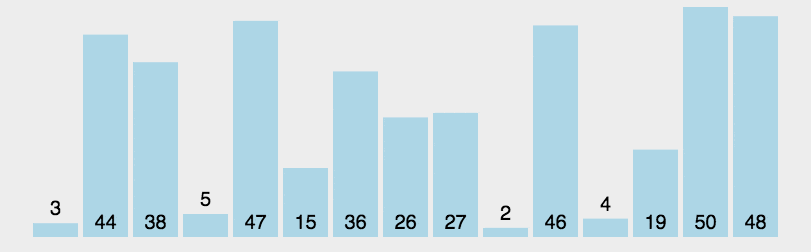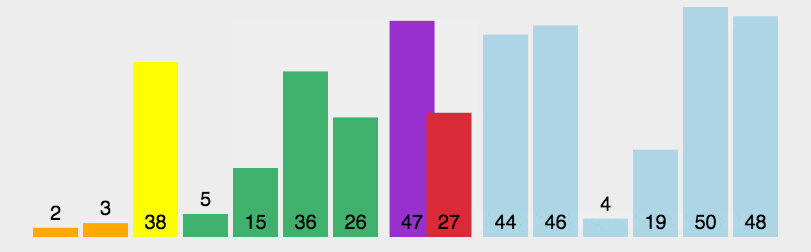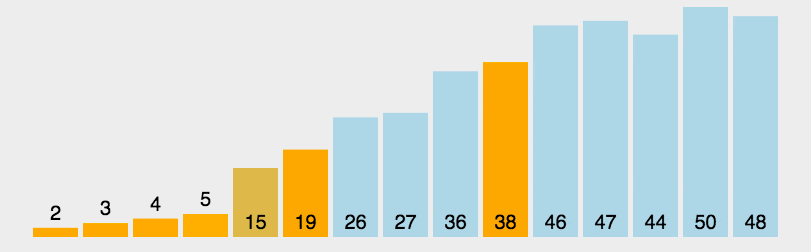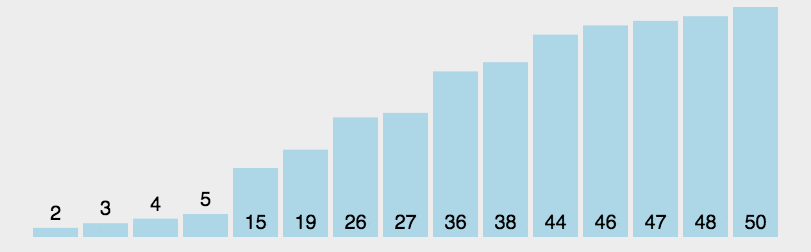
2. 例程 #
示例程序:
#include < iostream >
using namespace std;
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
void qsort(int l, int r)
{
int i = l;
int j = r;
int mid = a[(l + r) / 2];
do
{
while (a[i] < mid) i++;
while (a[j] > mid) j--;
if (i <= j)
{
swap(a[i], a[j]);
i++;
j--;
}
} while (i <= j);
if (l < j) qsort(l, j); // 递归
if (i < r) qsort(i, r);
}
int main()
{
qsort(0, 7);
for (int i=0; i < 8; ++i)
{
cout << a[i] << " ";
}
return 0;
}
3. 复杂度分析 #
在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
习题 #
请默写上述代码。




