主要内容 #

1. 算法讲解
2. 例程
3. 复杂度分析

1. 算法讲解 #

归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，是采用分治法（Divide and Conquer）的一个非常典型的应用。

1.1 计算步骤 #

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4. 重复步骤 3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

1.2过程模拟 #

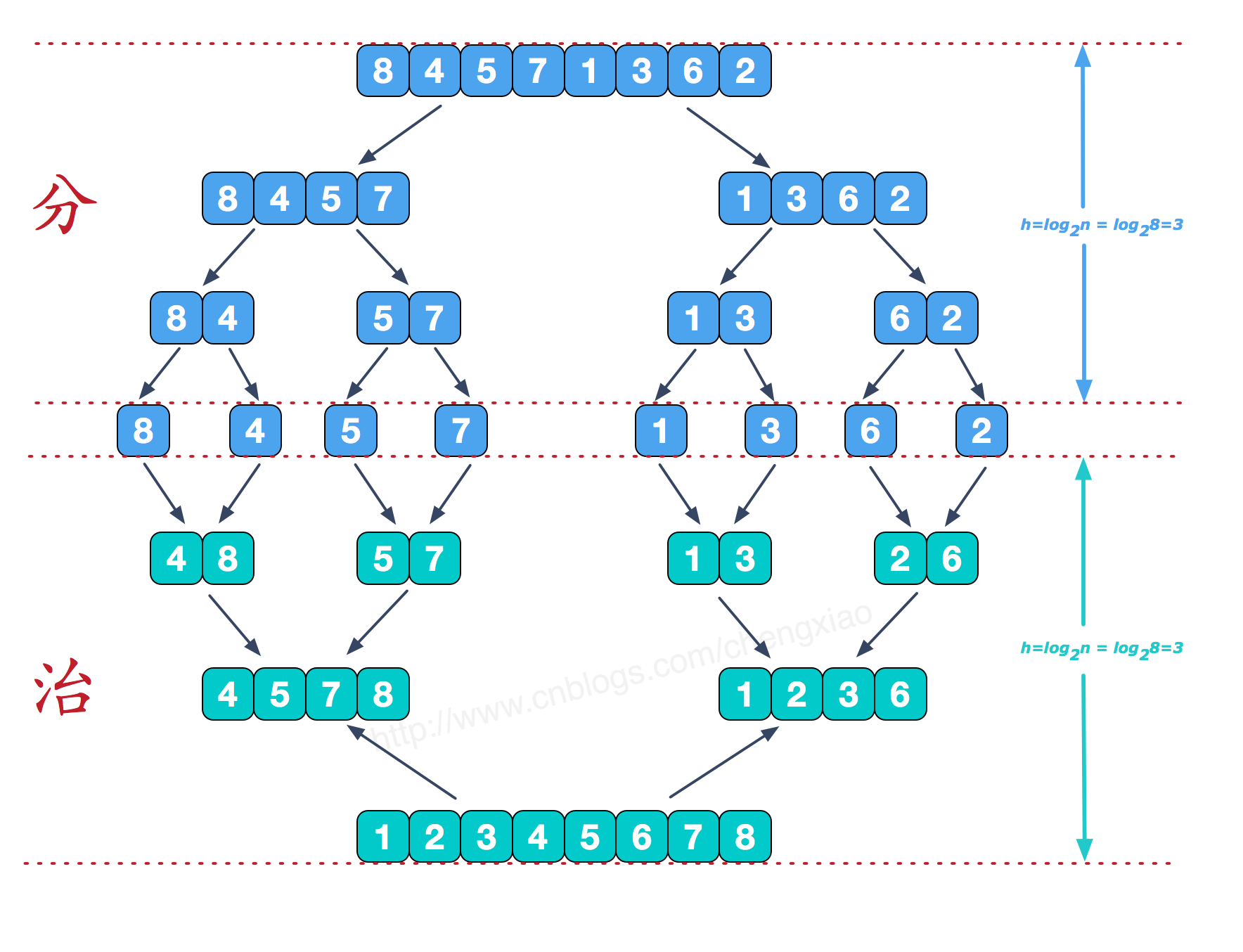
动画演示如下图所示：

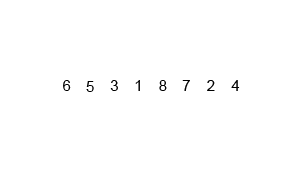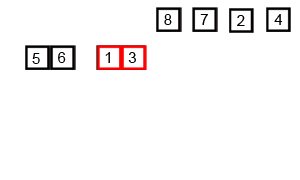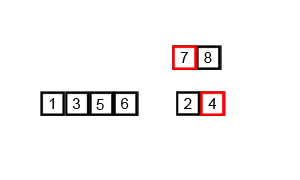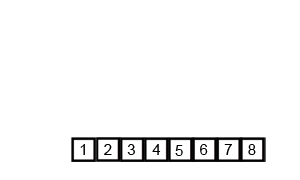
2. 例程 #

示例程序：

#include < iostream >
using namespace std;

int a[] = { 10,4,6,3,8,2,5,7 }; // 
int r[8] = { 0 }; // 是最终的结果

void msort(int s, int t)
{
    if (s == t)
        return; // 如果只有一个数字则返回，无需排序
    int mid = (s + t) / 2;
    msort(s, mid); // 分解左边序列
    msort(mid+1,t);// 分解右边序列

    int i = s, j = mid + 1, k = s; // 接下来合并
    while (i <= mid && j <= t)// i mid j t
    {
        if (a[i] <= a[j])
        {
            r[k] = a[i]; // 小的数，放在 r[k]中
            ++k;
            ++i;
        }
        else
        {
            r[k] = a[j];
            ++k;
            ++j;
        }
    }
    while (i <= mid) // 复制左边子序列剩余
    {
        r[k] = a[i];
        ++k;
        ++i;
    }
    while (j<=t) // 复制右边子序列剩余
    {
        r[k] = a[j];
        ++k;
        ++j;
    }
    for (int i = s; i <= t; i++)
        a[i] = r[i];

}

int main()
{
    msort(0,7);
    return 0;
}

3. 复杂度分析 #

比较操作的次数介于(n\log n)/2和 n\log n-n+1。 赋值操作的次数是2nlog n。

习题 #

请默写上述代码。