主要内容 #

1. 问题的提出
2. 深层的含义
3. 算法求解

1. 问题的提出 #

在西方，最先研究这个数列的人是比萨的列奥那多（意大利人斐波那契Leonardo Fibonacci），他描述兔子生长的数目时用上了这数列：
1. 第一个月初有一对刚诞生的兔子
2. 第二个月之后（第三个月初）它们可以生育
3. 每月每对可生育的兔子会诞生下一对新兔子
4. 兔子永不死去
假设在n月有兔子总共a对，n+1月总共有b对。在n+2月必定总共有a+b对：因为在n+2月的时候，前一月（n+1月）的b对兔子可以存留至第n+2月（在当月属于新诞生的兔子尚不能生育）。而新生育出的兔子对数等于所有在n月就已存在的a对

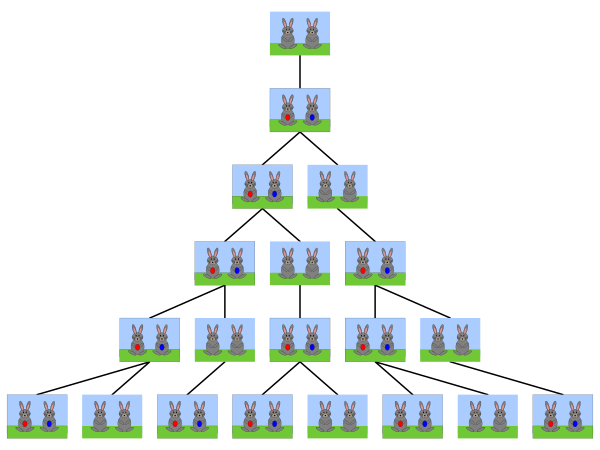
Fibonacci 数列的表达式为：
F(1)=1
F(2)=1
F(n) = F(n-1)+F(n-2)（n≥3）
经过计算，Fibonacci 数列的通项公式为：

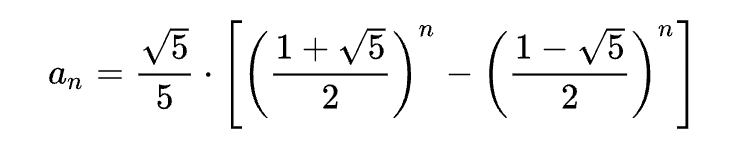
2. 深层的含义 #

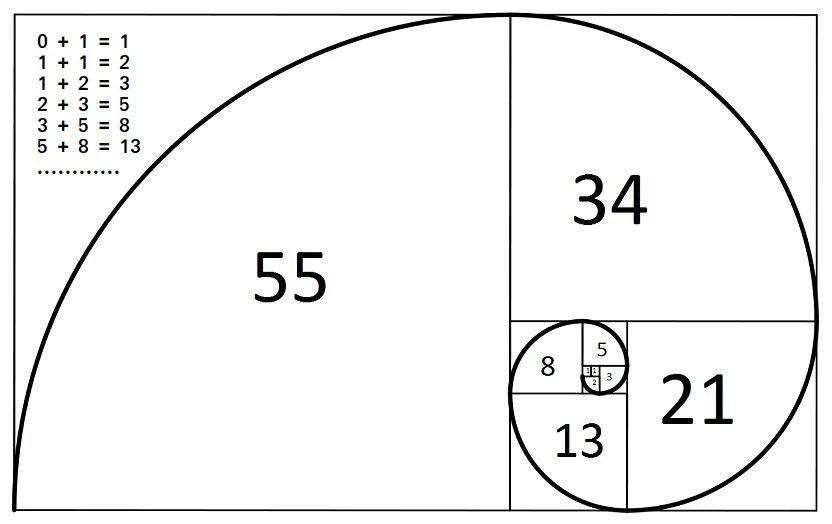
2.1 黄金分割数列 #

Fibonacci数列也被称为黄金分割数列，以Fibonacci数列为边长的正方形拼成的长方形越来越接近于黄金矩形(1:1.618)。
1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144、 233、 377、 610、 987……

2.2 杨辉三角形 #

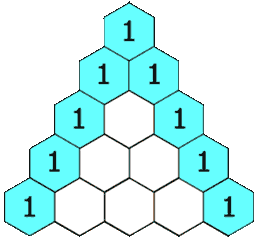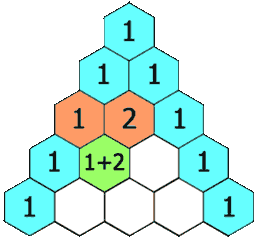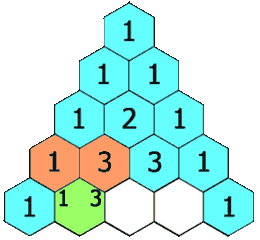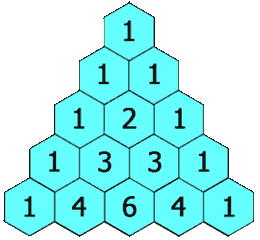
每个数是它左上方和右上方的数的和。
斐波纳契数也是杨辉三角形的每一条红色对角线上数字的和。

2.3 植物的生长 #

有些植物在生长点，即树枝形成或分裂的地方表达斐波那契数列。一个枝干生长后产生分支，会产生两个生长点。接下来，主枝干生成另一个分支，从而产生三个增长点。然后树干和第一分支产生两个增长点，使总数达到五个。此模式继续遵循斐波那契数。

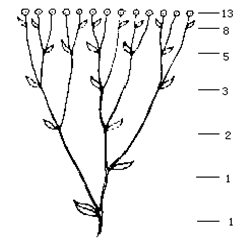
植物按照这样的方式生长将有利于进行光合作用。
此外，如果你计算花上的花瓣数，通常会发现花瓣的总数就是斐波那契数列中的数字之一。例如，百合和鸢尾有三个花瓣，金凤花和野玫瑰有五个花瓣，飞燕草有八瓣等等。
还有菠萝、松子等，也都符合这个特点，一般会出现34,55，89和144这几个数字。
Fibonacci数列虽然简单但是是数学当中非常重要的数列。

3. 算法求解 #

#include < iostream >
using namespace std;
int main(){
    int x, y, n;
    x = 1;
    y = 0;
    for(int i = 0; i < n; ++i){
        x = x + y;
        y = x - y;
    }
    cout << y << endl;
    return 0;
}