主要内容 #

1. 问题介绍
2. 求解方法
3. 编程计算
4. 问题延伸

1. 问题介绍 #

n条封闭曲线，任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成的区域个数。

2. 求解方法 #

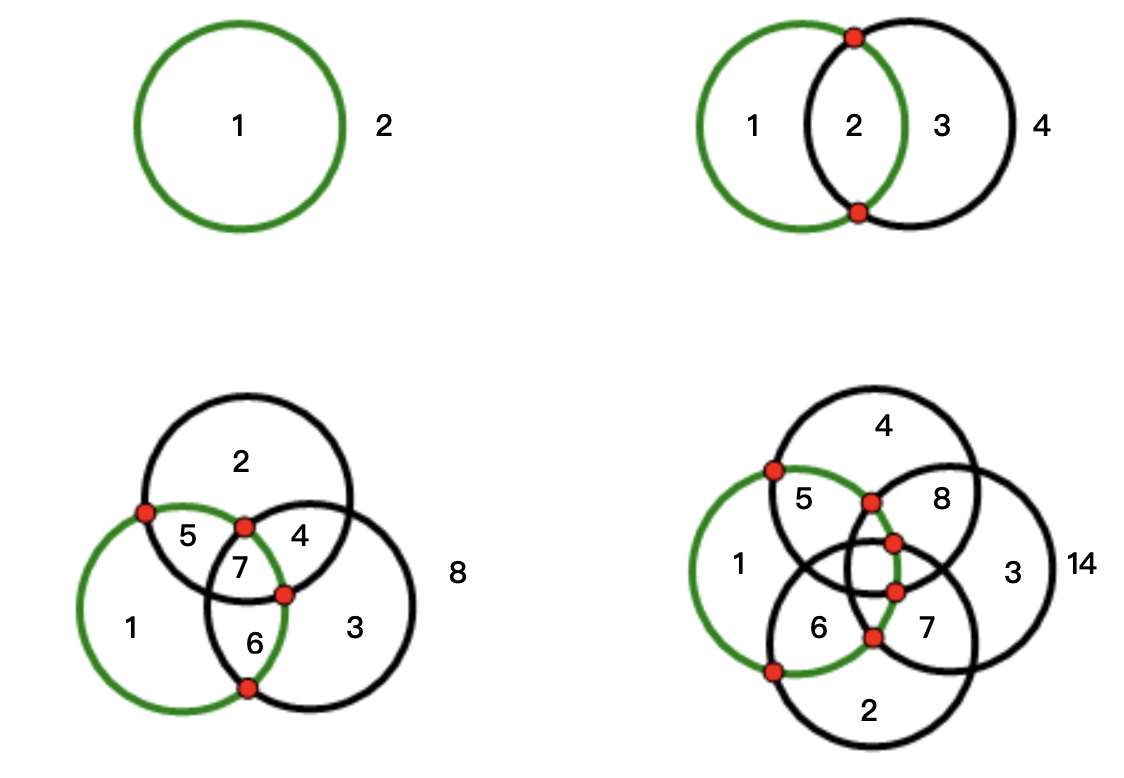
假设A(n)为n条封闭曲线把平面分割成的区域个数，如上图所示，A(2)-A(1)=2，A(3)-A(2)=4，A(4)-A(3)=6。
从这些式子中可以看出A(N)-A(N-1)=2(N-1)。
试着推导一下：
当平面中有N-1条曲线将平面分割成A(N-1)个区域后，第N-1条曲线每与曲线相交一次，就会增加一个区域，因为平面中已经有N-1条封闭曲线，而且，不会与任意两条曲线相交于一点，故平面中增加了2(N-1)个区域，加上已有的A(N-1)个区域，故一共有A(N-1)+2(N-1)个区域。所以递推关系式为：A(N)=A(N-1)+2(N-1)，边界条件是A(1)=2。

3. 编程计算 #

参考程序

#include < iostream >
int main(){
    int x, y, n;
    cin >> n;
    if(n == 1){
        cout << 2 << endl;
        return 0;
    }
    x = 2;
    y = 0;
    for(int i = 1; i < n; ++i){
        y = x + 2 * i;
        x = y;
    }
    cout << y << endl;
    return 0;
}

4. 问题延伸 #

问题：n条直线，最多可以把平面分为多少个区域。

解：当有n-1条直线时，平面最多被分成了f(n-1)个区域。则第n条直线要是切成的区域数最多，就必须与每条直线相交且不能有同一交点。 这样就会得到n-1个交点。这些交点将第n条直线分为2条射线和n-2条线段。而每条射线和线段将以有的区域一分为二。这样就多出了2+(n-2)个区域。
如下图所示：第四条红色的线与其他3条线生成了3个交点，生成了两条射线两条线段，这两条射线两条线段将下面的区域被分成了四份，即多出了四个区域。

所以：f(n)=f(n-1)+n
递推公式：f(n)=n(n+1)/2+1。
请自行编程计算上述问题。