主要内容 #

1. 问题介绍
2. 求解方法
3. 编程计算

1. 问题介绍 #

卡塔兰数(Catalan)是组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡特兰（1814–1894）命名。历史上，清朝数学家明安图（1692年－1763年）在其《割圜密率捷法》中最先发明这种计数方式，远远早于卡塔兰。有中国学者建议将此数命名为“明安图数”或“明安图-卡塔兰数”。
问题的提出：在一个凸n边形中，通过不相交于n边形内部的对角线，把n边形拆分成若干三角形，不同的拆分方式用h(n)表示，h(n)即为Catalan数。例如n=6的分法如下：

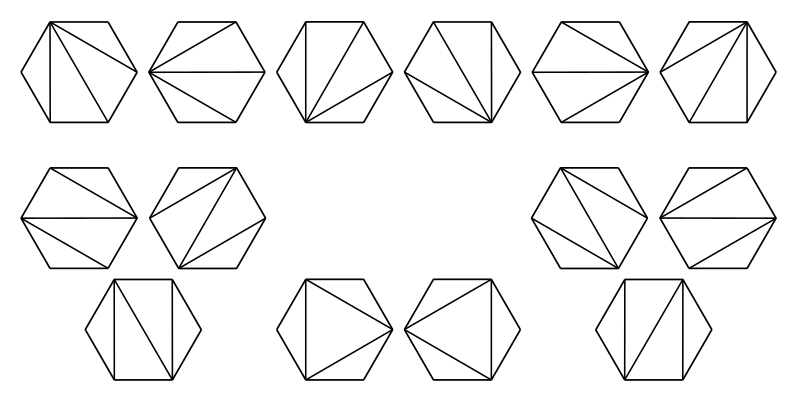
从零开始，卡特兰数的前几项为1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,35357670,129644790…

2. 求解方法 #

因为凸多边形的任意一条边必定属于某一个三角形，所以我们以某一条边为基准，以这条边的两个顶点为起点P1和终点Pn（P即Point），将该凸多边形的顶点依序标记为P1、P2、……、Pn，再在该凸多边形中找任意一个不属于这两个点的顶点Pk（2<=k<=n-1），来构成一个三角形，用这个三角形把一个凸多边形划分成两个凸多边形，其中一个凸多边形，是由P1，P2，……，Pk构成的凸k边形（顶点数即是边数），另一个凸多边形，是由Pk，Pk+1，……，Pn构成的凸n-k+1边形。
此时，我们若把Pk视为确定一点，那么根据乘法原理，f（n）的问题就等价于——凸k多边形的划分方案数乘以凸n-k+1多边形的划分方案数，即选择Pk这个顶点的f（n）=f（k）×f（n-k+1）。而k可以选2到n-1，所以再根据加法原理，将k取不同值的划分方案相加，得到的总方案数为：f（n）=f（2）f（n-2+1）+f（3）f（n-3+1）+……+f（n-1）f（2）。
设h(n)为catalan数的第n项，令h(0)=1,h(1)=1，catalan数满足递推式  ：
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)*h(0) (n≥2)
例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
看到此处，再看看卡特兰数的递推式，答案不言而喻，即为f（n）=h（n-2） （n=2，3，4，……）。
最后，令f（2）=1，f（3）=1。
实际上，Catalan数的另外一个递推关系式为：
f(n)=(4n-2)/(n+1)f(n-1)。

3. 编程计算 #

参考程序

#include < iostream >
using namespace std;
int main(){
    int n;
    cin >> n;
    if(n <= 1){
        cout << 1 << endl;
        return 0;
    }
    double x = 1.0;
    double y = 1.0;
    for(int i = 2; i < n; ++i){
        y = (4.0*i - 2.0)/(i + 1.0) * x;
        x = y;
    }
    cout << y << endl;
    
    return 0;
}