主要内容 #

1. 问题介绍
2. 求解方法
3. 编程计算

1. 问题介绍 #

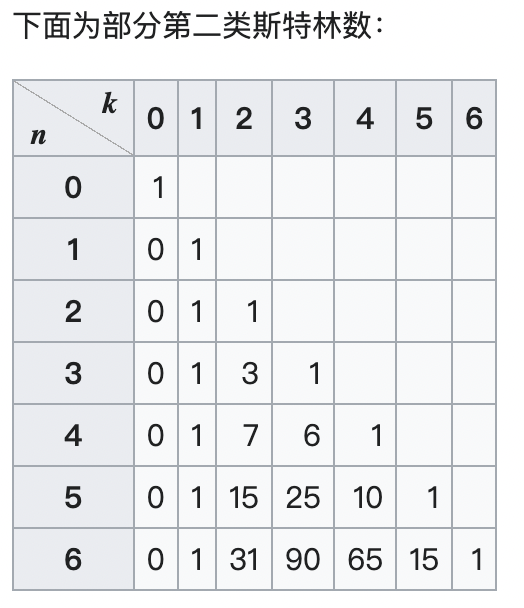
n个有区别的球放在k个相同的盒子中，要求无一空盒，其不同的方案用S(n,k)表示，称为Stirling数。
例如：
将n个球分成k组的分组方法的数目。例如有甲、乙、丙、丁4个球，若所有球分成1组，只能所有人在同一组，因此S(4,1)=1；若所有球分成4组，只能每人独立一组，因此S(4,4)=1；若分成2组，可以是甲乙一组、丙丁一组，或甲丙一组、乙丁一组，或甲丁一组、乙丙一组，或其中三人同一组另一人独立一组，即：

• {甲, 乙}{丙, 丁}
• {甲, 丙}{乙,丁}
• {甲, 丁}{乙, 丙}
• {甲}{乙, 丙, 丁}
• {乙}{甲, 丙, 丁}
• {丙}{甲, 乙, 丁}
• {丁}{甲, 乙, 丙}

因此，S(4,2)=7。同理，S(4,3)=6。

2. 求解方法 #

有n个球分别用b1, b2, ···, bn表示。从中取出1个球bn，bn的放法有以下两种：
第一种：bn独占一个盒子，那么剩下的球只能防止m-1个盒子中，方案数为S(n-1,k);
第二种：bn与其他球共占一个盒子，那么可以事先将b1，b2， ···，bn-1这n-1个球放入m个盒子中，然后将bn放入其中一个盒子中，方案数为
mS(n-1,k)。
综合以上两种情况，可以得出第二类Stirling数定理：
S(n,k)=kS(n-1,k)+S(n-1,k-1);
边界条件可以由定义推导出：
S(n,0)=0; S(n,1)=1; S(n,n)=1; S(n,k)=0(k>n)。

3. 编程计算 #

参考程序

#include < iostream >
using namespace std;

int main(){
    //存放所有的组合
    int S[101][101];
    //设置边界条件
    for(int i = 0; i < 101; ++i){
        for(int j = 0; j < 101; ++j){
            if(j == i){
                S[i][j] = 1;
            }else if(j > i){
                S[i][j] = 0;
            }else if(j == 1){
                S[i][j] = 1;
            }else if(i > 0 && j > 0){
                S[i][j] = j*S[i-1][j] + S[i - 1][j-1];
            }
        }
    }
    int n, k;
    //输入参数n和k
    cin >> n >> k;
    //输出结果
    cout << S[n][k] << endl;
}